卷积神经网络 - 岁杪二四

两个原则？ 平移不变性和局部性

重新考察全连接层#

将输入和输出变形为矩阵（宽度，高度）
将权重变形为4-D张量 $(h,w)$ 到 $(h',w')$
$_{i,j}=\sum_{k,l}w_{i,j,k,l}x_{k,l}=\sum_{a,b}v_{i,j,a,b}x_{i+a,j+b}$
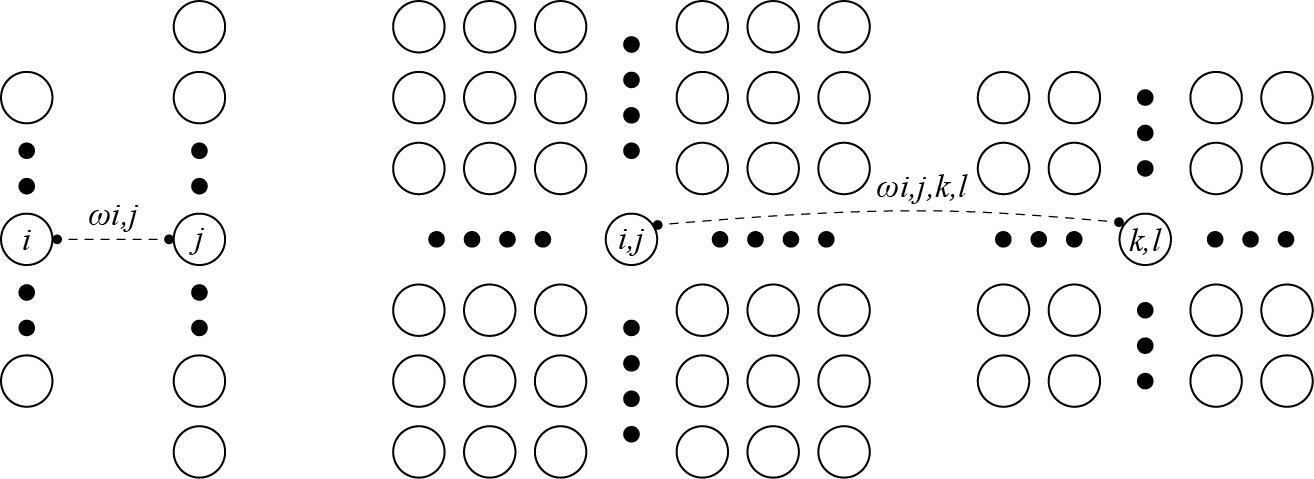
$v$ 是 $w$ 的重新索引 $v_{i,j,a,b}=w_{i,j,i+a,j+b}$

原则 #1 - 平移不变性#

$x$ 的平移导致 $h$ 的平移 $h_{i,j}=\sum_{a,b}v_{i,j,a,b}x_{i+a,j+b}$
$v$ 不应该依赖于 $(i,j)$
解决方案： $v_{i,j,a,b}=v_{a,b}$ $_{i,j}=\sum_{a,b}v_{a,b}x_{i+a,j+b}$
这就是2维交叉相关

原则 #2 - 局部性#

h_{i,j}=\sum_{a,b}v_{a,b}x_{i+a,j+b}

当评估 $h_{i,j}$ 时，我们不应该用远离 $x_{i,j}$ 的参数
解决方案：当 $|a|,|b| > \Delta$ 时，使得 $v_{a,b}=0$ $_{i,j}=\sum_{a=-\Delta}^{\Delta}\sum_{b=-\Delta}^{\Delta}v_{a,b}x_{i+a,j+b}$

总结#

卷积层将输入和核矩阵进行交叉相关，加上偏移后得到输出
核矩阵和偏移时可学习的参数
核矩阵大小是超参数

填充#

NOTE
对图像进行一次卷积操作后，输出的矩阵相较于输入的矩阵会变小。假设给定 $(32\times 32)$ 的输入图像，应用 $5\times 5$ 大小的卷积核：
第1层得到输出大小为 $28 \times 28$
第7层得到输出大小为 $4\times 4$ 如果用更大的卷积核，则输出矩阵的缩小会变得更快，形状会从 $n_h\times n_w$ 减少到 $(n_h-k_h+1)\times (n_w-k_w+1)$

为了解决这个缩小的问题，我们选择在输入周围添加额外的行/列填充 $p_h$ 行和 $p_w$ 列，输出的形状为 $(n_h-k_h+p_h+1)\times (n_w-k_w+p_w+1)$ 通常取 $p_h=k_h-1$ ， $p_w=k_w-1$ ：

当 $k_h$ 为奇数：在上下两侧填充 $p_h/2$
当 $k_h$ 为偶数：在上侧填充 $\lceil p_h/2 \rceil$ ，在下侧填充 $\lfloor p_h/2 \rfloor$

步幅#

填充减小的输出大小与层数线性相关，给定输入大小 $224 \times 224$ ，在使用 $5 \times 5$ 卷积核的情况下需要 $44$ 层将输出降低到 $4\times 4$ 需要大量的计算才能得到较小输出

步幅是指行/列的滑动步长，例：高度3宽度2的步幅当垂直步幅为 $s_h$ 、水平步幅为 $s_w$ 时，输出形状为 $\lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor$ 如果我们设置了 $p_h=k_h-1$ 和 $p_w=k_w−1$ ，则输出形状将简化为

\lfloor(n_h+s_h-1)/s_h\rfloor \times \lfloor(n_w+s_w-1)/s_w\rfloor

更进一步，如果输入的高度和宽度可以被垂直和水平步幅整除，则输出形状将为

$(n_h/s_h) \times (n_w/s_w)$

IMPORTANT
填充和步幅是卷积层的超参数
填充在输入周围添加额外的行/列，来控制输出形状的减少量
步幅是每次滑动核矩阵时的行/列步长，可以成倍地减少输出形状