暑假集训第二篇周记(7月17日-7月23日)
摘要
涉及内容:函数和递归、结构体和STL入门
每日知识点
第一天 7月17日:函数和递归
1.1简单函数的编写
引入:计算两点欧几里德距离的函数
double dist(double x1, double y1, double x2, double y2)
{
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
- C语言中的数学函数可以定义成 “返回类型 函数名(参数列表){ 函数体 }” ,其中函数体的最后一条语句应该是 “return 表达式;” 。
- 函数的参数和返回值最好是“一等公民”
int或double(注意char是一种特殊的int)。其他“非一等公民”作为以参数和返回值要复杂一些。 - 如果函数在执行的过程中碰到了
return语句,将直接退出这个函数,不去执行后面的语句。相反,如果在执行过程中始终没有return语句,则会返回一个不确定的值。 main函数是有返回值的,请总是让main函数返回。
下面给出上述函数的另一种方法:
double dist(double x1, double y1, double x2, double y2)
{
double dx=x1-x2;
double dy=y1-y2;
return hypot(dx,dy); // hypot函数头文件math.h或cmath
// hypot(a,b)的返回值为double类型
}
提示
hypot函数的功能是计算——直角三角形斜边的长度。
函数
hypot(x,y)表示根据直角三角形的两直角边长度和计算其斜边的长度。或者是从标点(x,y)到原点的距离,该函数的算法等同于
sqrt(x*x+y*y)。
1.2 使用结构体的函数
struct Point{ double x, y; };
double dist(struct Point a, struct Point b)
{
return hypot(a.x-b.x, a.y-b.y);
}
在C语言中,定义结构体的方法为:“struct 结构体名称{ 域定义 };”,注意花括号的后面还有一个分号。
为了方便,往往用 "typedef struct{ 域定义 }类型名;" 的方式定义一个新类型名。这样,就可以像原生数据类型一样使用这个自定义类型。
1.3 应用举例
孪生素数 如果和都是素数,则称它们是孪生素数。输入,输出两个数均不超过m的最大孪生素数。。例如时答案是、,时答案是、。
#include <stdio.h>
#include <math.h>
#include <assert.h>
int is_prime(int x){
int i, m;
assert(x >= 0); //使用断言,防止x<0
if(x == 1) return 0;
m = floor(sqrt(x) + 0.5);
for(i = 2; i <= m; i++)
if(x % i == 0) return 0;
return 1;
}
int main(){
int i, m;
scanf("%d", &m);
for(i = m-2; i >= 3; i--)
if(is_prime(i) && is_prime(i+2)) {
printf("%d %d\n", i, i+2);
break;
}
return 0;
}
提示
程序使用了 assert.h的 assert宏来限制非法的函数调用:当不成立时,程序将异常终止,并给出了提示信息。
断言assert 的语义如下:如果表达式的值为(假),则输出错误消息并终止程序的执行(一般还会出对话框,说明在什么地方引发了assert);如果表达式为真,则不进行任何操作。因此,断言失败就表明程序存在一个bug。
2 变量的作用域和变量的生存区
变量的作用域:即变量的作用范围(或有效范围)。分为:局部变量和全局变量 变量的生存区:变量从被生成到被撤销的这段时间。即变量占用内存的时间。分为动态变量和静态变量
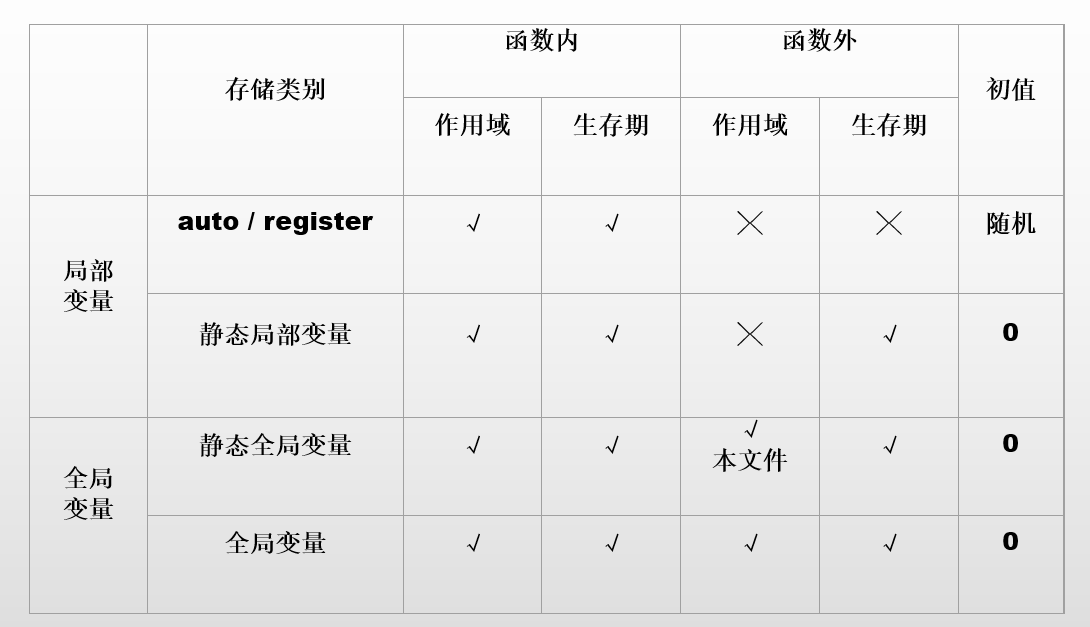
3.1递归的定义和递归函数
基本概念:一个函数在它的函数体内调用它自身称为递归调用。这种函数称为递归函数。C语言允许函数的递归调用。在递归调用中,主调函数又是被调函数。执行递归函数将反复调用其自身,每调用一次就进入新的一层。
递归函数的构成要素: 递归函数必须满足两个条件:
- 必须有一个终止准则(递归的边界条件、递归的结束条件);
- 在每一次调用自己时,必须是(在某种意义上)更接近于解(递推公式或递归方程);
边界条件与递归方程是递归函数的二个要素。若没有条件1,则递归无从终止;若没有条件2,则不是递归。
递归调用过程(两个阶段):
(1)递推阶段
将原问题不断地分解为新的子问题,逐渐从未知的向已知的方向推进,最终达到已知的条件,即递归结束条件,这时递推阶段结束。
(2)回归阶段
从已知条件出发,按照“递推”的逆过程,逐一求值回归,最终到达“递推”的开始处,结束回归阶段,完成递归调用。
第二天 7月18日:结构体和STL入门
结构体(Struct)是一种用户自定义的数据类型,可以将多个不同类型的数据组合在一起形成一个新的数据类型。结构体可以用来表示具有相关属性的实体或对象,方便对其进行管理和操作。
类似于:
struct name{
int x;
char y;
};
结构体的定义通常在函数外部进行,可以在全局范围内访问。
#include <iostream>
using namespace std;
// 定义一个学生结构体
struct Student {
string name;
int age;
double gpa;
};
int main() {
// 声明一个学生结构体变量
Student s;
// 给学生结构体的成员赋值
s.name = "Alice";
s.age = 20;
s.gpa = 3.8;
// 输出学生结构体的成员
cout << "Name: " << s.name << endl;
cout << "Age: " << s.age << endl;
cout << "GPA: " << s.gpa << endl;
return 0;
}
在上面的示例中,我们定义了一个名为Student的结构体,包含了学生的姓名、年龄和 GPA。在main函数中,我们声明了一个Student类型的变量s,并使用点操作符对结构体的成员进行赋值和访问。
结构体可以作为参数传递给函数,也可以作为函数的返回值。通过结构体,我们可以更方便地组织和操作多个相关的数据。
第三天 7月19日:STL:vector(向量)、stack(栈)、queue(列队)
STL泛性编程 ->模板类和模板函数
容器的分类:
- 序列式容器:每个元素都有固定的位置,取决于插入的时机和地点:vector 、deque、list、stack、queue
- 关联式容器:元素位置取决于特定的排序准则和插入顺序无关:set、multiset、map、multimap
vector:置于一个动态数组中加以管理的容器 特点是:在尾部插入元素比较快
vector<int> v1; //一个存放int类型数据的vector容器
vector<CA*> vecpCA; //用于存放CA对象的指针的vector容器
提示
尖括号内还可以设置指针或者自定义数据类型
可以采用下标方式、vector.at()、迭代器方式访问vector容器中的元素,以下是vector容器的部分基本函数
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> v; // 定义一个空的整数向量
// 添加元素
v.push_back(1); // 在向量的末尾添加元素1
v.push_back(2); // 在向量的末尾添加元素2
// 获取元素
cout << "First Element: " << v.front() << endl; // 输出第一个元素1
cout << "Last Element: " << v.back() << endl; // 输出最后一个元素2
// 修改元素
v[0] = 3; // 将第一个元素修改为3
// 删除元素
v.pop_back(); // 删除向量末尾的元素,向量变为[3]
// 获取容器的大小
cout << "Size: " << v.size() << endl; // 输出向量的大小为1
// 判断容器是否为空
if (v.empty()) {
cout << "Vector is empty" << endl;
} else {
cout << "Vector is not empty" << endl; // 输出向量不为空
}
// 清空容器
v.clear(); // 清空向量,向量变为空
return 0;
}
stack:提供了一种后进先出(Last-In-First-Out, LIFO)的数据结构。stack通过封装已有的容器(默认是 deque)实现了栈的功能,使得栈的操作更加方便。栈通常用于在函数调用和递归等场景中,记录临时的数据和状态。
以下是stack的部分基本函数:
#include <iostream>
#include <stack>
using namespace std;
int main() {
stack<int> s; // 定义一个整型栈
// 压入元素
s.push(1); // 将元素1压入栈顶
s.push(2); // 将元素2压入栈顶
// 获取栈顶元素
cout << "Top Element: " << s.top() << endl; // 输出栈顶元素2
// 弹出栈顶元素
s.pop(); // 弹出栈顶元素,栈变为[1]
// 获取栈的大小
cout << "Size: " << s.size() << endl; // 输出栈的大小为1
// 判断栈是否为空
if (s.empty()) {
cout << "Stack is empty" << endl;
} else {
cout << "Stack is not empty" << endl; // 输出栈不为空
}
// 清空栈
while (!s.empty()) {
s.pop(); // 弹出栈中所有元素,使栈变为空
}
return 0;
}
queue:提供了一种 先进先出(First-In-First-Out, FIFO) 的数据结构。queue通过封装已有的容器(默认是 deque)实现了队列的功能,使得队列的操作更加方便。队列通常用于任务调度、缓冲区等场景中。
以下是queue的部分基本函数:
#include <iostream>
#include <queue>
using namespace std;
int main() {
queue<int> q; // 定义一个整型队列
// 入队操作
q.push(1); // 将元素1添加到队列的末尾
q.push(2); // 将元素2添加到队列的末尾
// 获取队首元素
cout << "Front Element: " << q.front() << endl; // 输出队首元素1
// 出队操作
q.pop(); // 将队首元素出队,队列变为[2]
// 获取队列的大小
cout << "Size: " << q.size() << endl; // 输出队列的大小为1
// 判断队列是否为空
if (q.empty()) {
cout << "Queue is empty" << endl;
} else {
cout << "Queue is not empty" << endl; // 输出队列不为空
}
// 清空队列
while (!q.empty()) {
q.pop(); // 将队列中所有元素出队,使队列变为空
}
return 0;
}
第四天:7月20日:STL:deque(双端队列)、priority_queue(优先队列)、list(链表)、set(集合)、map(映射)、pair
deque:是一种具有队列和栈性质的数据结构,可以理解为queue的功能优化版,两头都可以进行插入、读取
以下是deque的部分基本函数:(queue中出现过的函数不再写)
deque<int> dq; // 定义一个整型双端队列
dq.pop_front(); // 弹出队首元素
dq.pop_back(); // 弹出队尾元素
// 判断队列是否为空
if (dq.empty()) {
cout << "Deque is empty" << endl;
} else {
cout << "Deque is not empty" << endl; // 输出队列不为空
}
dq.clear(); // 清空队列
priority_queue:优先级最高的先出队(初始化为从大到小,可重载)。队列和排序的完美结合,不仅可以存储数据,还可以将这些数据按照设定的规则进行排序。每次的push和pop操作,优先队列都会动态调整,把优先级最高的元素放在前面。
以下是优先队列的部分基本函数:
priority_queue<int> pq; // 定义一个整型优先队列
pq.top();//返回具有最高优先级的元素值,但不删除该元素
pq.pop();//删除最高优先级元素
// 清空队列(注意:优先队列没有clear函数,可以通过重新赋值一个空的优先队列来实现清空)
pq = priority_queue<int>(); // 清空队列,队列变为空
STL中,优先队列是使用二叉堆来实现的,往往列队中push入一个数或者pop一个数,复杂度是O(logn)。
list:双向链表。内存空间不必连续,通过指针来进行数据的访问,高效率地在任意地方删除和插入
list和vector的优缺点正好相反,他们的应用场景不同:
- vector:插入和删除操作少(O(n)),随机访问元素频繁(O(1))
- list:插入和删除频繁(O(1)),随机访问较少(O(n))
以下是链表的部分基本函数:
#include <iostream>
#include <list>
using namespace std;
int main() {
list<int> lst; // 定义一个整型链表
// 在链表末尾插入元素
lst.push_back(1); // 将元素1插入到链表末尾
lst.push_back(2); // 将元素2插入到链表末尾
// 在链表头部插入元素
lst.push_front(3); // 将元素3插入到链表头部
lst.push_front(4); // 将元素4插入到链表头部
// 删除链表中的某个元素
lst.remove(2); // 删除链表中值为2的元素,链表变为[4, 3, 1]
// 获取链表的大小
cout << "Size: " << lst.size() << endl; // 输出链表的大小为3
// 判断链表是否为空
if (lst.empty()) {
cout << "List is empty" << endl;
} else {
cout << "List is not empty" << endl; // 输出链表不为空
}
// 清空链表
lst.clear(); // 清空链表,链表变为空
return 0;
}
set:用二叉搜索树实现,集合中的每个元素只出现一次且是排好序的。set像一个一直在排序的,插入更慢的,无法通过下标找元素的vector
以下是set的部分基本函数:
set<Type> A;//定义
A.insert(item);//把item放进set
A.erase(item);//删除元素item
A.clear();//清空set
A.size();
A.clear();
A.find(k);//返回一个迭代器,指向键值k
multiset与set的唯一区别就是不去重
map:关联容器,实现从键(key)到值(value)的映射,元素数据是由一个键值和一个映照数据组成的,键值与映照数据之间具有一一对应关系。会像set一样对键插入时自动排序。
以下是set的部分基本函数:
#include <iostream>
#include <map>
using namespace std;
int main() {
map<string, int> mp; // 定义一个映射,key为字符串,value为整型
// 插入元素
mp["apple"] = 3; // 插入一个key-value对,key为"apple",value为3
mp["banana"] = 2; // 插入一个key-value对,key为"banana",value为2
mp["orange"] = 5; // 插入一个key-value对,key为"orange",value为5
// 查找元素
if (mp.find("banana") != mp.end()) {
cout << "Element 'banana' found in the map with value: " << mp["banana"] << endl;
} else {
cout << "Element 'banana' not found in the map" << endl;
}
// 删除元素
mp.erase("apple"); // 删除key为"apple"的元素
// 获取映射的大小
cout << "Size: " << mp.size() << endl; // 输出映射的大小为2
// 判断映射是否为空
if (mp.empty()) {
cout << "Map is empty" << endl;
} else {
cout << "Map is not empty" << endl; // 输出映射不为空
}
// 清空映射
mp.clear(); // 清空映射,映射变为空
return 0;
}
pair:
是一种模板类型,其中包含两个数据值,两个数据类型可以不同,基本的定义如下:
pair<int,string> a;
表示a有两个类型,第一个元素是int类型,第二个元素是string类型,如果创建pair没有对其进行初始化,则调用默认构造函数对其初始化。
pair<string,string> a("James","Joy");//也可以像这样直接对其初始化
由于pair类型的使用比较繁琐,因为如果要定义多个形同的pair类型的时候,可以使用 typedef或 define简化声明:
typedef pair<string,string> author;
author pro("May","Lily");
author joye("James","Joyce");
对于pair类,由于它只有两个元素,分别命名为first和second,因此直接使用普通点操作符即可访问其成员
pair<string,string> a("Lily","Poly");
string name;
name = pair.second;
生成新的pair对象:可以使用 make_pair对已存在的两个数据构造一个新的pair类型:
int a = 8;
string m = "James";
pair<int,string>newone;
newone = make_pair(a,m);
next_permutation
next_permutation(): 求”下一个“排列组合。
例如三个字符{a,b,c}组成的序列,next_permutation()能按照字典序返回六个组合:abc, acb, bac, bca, cab, cba
函数next_permutation()的定义有两种形式:
bool next_permutation(first,last);
bool next_permutation(first,last,Compare comp);
返回值:如果没有下一个排列组合,返回false,否则返回true。每次执行next_permutation()一次,会把新的排列放到原来的空间里。
排列的范围:[first,last),包括first,不包括last。
部分题目详细分析与总结
第一天 7月17日:函数和递归
第一题:显示菱形(递归版)
请编写函数,显示菱形。
函数原型:void Diamond(int height, char symbol);
说明:参数 height 为菱形的高,symbol 为显示字符。函数将在屏幕上显示高度和底宽为 height 由字符 symbol 组成的菱形。若 height 为偶数,或者小于等于 0,则不输出。
提示:需要利用前面作业中的 Show 函数、IsOdd 函数或 IsEven 函数,此外需要增加自用的内部函数。
裁判程序
#include <stdio.h>
int IsOdd(int number);
int IsEven(int number);
void Show(int number, char symbol);
void Diamond(int height, char symbol);
int main()
{
int n;
char s;
scanf("%d %c", &n, &s);
Diamond(n, s);
return 0;
}
......
/* 你提交的代码将被嵌在这里 */
Input1: 5 @
output1:
@
@@@
@@@@@
@@@
@
Input2: 3 #
output2: (无输出)
答案:
void TriAngle(int pos, int height, char symbol, int dir)
{
if(height==0) return;
if(dir>0)//打印上三角
{
TriAngle(pos+1,height-1,symbol,dir);//先进行递归打印,右移一格,打印个数减二
Show(pos,' ');Show(2*height-1,symbol);Show(1,'\n');//最后才进行最终的打印
}else{
//打印下三角
Show(pos,' ');Show(2*height-1,symbol);Show(1,'\n');//先进行最终的打印
TriAngle(pos+1,height-1,symbol,dir);//后进行递归打印,右移一格,打印个数减二
}
}
void Diamond(int height, char symbol)
{
if(height<=0||IsEven(height))return;
TriAngle(1,height/2,symbol,1);//打印上三角
Show(height,symbol);Show(1,'\n');//打印中间
TriAngle(1,height/2,symbol,-1);//打印下三角
}
第二天 7月18日:结构体和STL入门
第一题:F - Zone Selection
在地图中,共有台密码机,第 台密码机的坐标为 。在推广化的游戏中,有 名求生者。每名求生者可以选择一台密码机作为其出生点,我们称被选择的密码机为出生密码机。
监管者共有 个出生点可供选择。第 个可能的出生点坐标为 。此时,由于“封禁”天赋的存在,离监管者最远的密码机将不能被破译。
如果多台密码机与监管者的距离相同且最远,“封禁”天赋将会封禁这几台密码机中标号最小的那一台。
请问在该 个出生点中,有多少出生点可以使某一台出生密码机被封禁。
请注意:坐标点 与坐标点 之间的距离为
Input:
输入共 +++1 行。
输入的第一行为三个整数 ,,。
接下来行,每行两个整数 ,,表示一台密码机的坐标。
接下来行,每行两个整数 ,,表示一名求生者选择出生密码机的坐标,保证该坐标在上面出现过。
接下来行,每行两个整数 ,,表示监管者的一个出生点。
Output: 输出一行一个整数,为答案。
Sample1:
Input Output
4 2 2 1
-1 0
0 -1
2 0
0 2
-1 0
0 2
3 0
0 0
提示
【样例 #1 解释】
显然,第一台密码机和第四台密码机为出生密码机。
第一位监管者与位置在 (-1, 0) 的第一台密码机距离最远,为 4。因此,第一台密码机被封禁。
第二位监管者与位置在 (2, 0) 或 (0, 2) 的第三、四台密码机距离相同且最远,为 2。根据上面提到的规则,第三台密码机被封禁。
被封禁的出生密码机为 1 台。
【数据规模与约定】
- 对前 10% 的数据,保证。
- 对前 20% 的数据,保证,,≤。
- 对另外 20% 的数据,保证密码机与出生点的坐标中的均为0。
- 对另外 10% 的数据,保证。
- 对另外 10% 的数据,保证。
- 对于 100% 的数据范围 ≤≤,≤≤,≤≤, ≤| |, | |≤ 。
#include <stdio.h>
#include <math.h>
struct code{
int id;
int x;
int y;
int flag;
double d;
} c[1000];
struct dmax{
int t;
int id;
double d;
} max;
double far(int x1, int y1, int x2, int y2){
return sqrt(1.0 * ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)));
}
int main()
{
int n, k, T;
scanf("%d%d%d", &n, &k, &T);
int count = 1;
// 输入第一组 n 个密码机的坐标
for (int i = 0; i < n; i++){
scanf("%d%d", &c[i].x, &c[i].y);
c[i].flag = 0; // 初始化为未标记
c[i].id = count;
count++;
}
// 输入第二组 k 个密码机的坐标,并进行标记
for (int i = 0; i < k; i++){
int x, y;
scanf("%d%d", &x, &y);
for (int j = 0; j < n; j++){
if (x == c[j].x && y == c[j].y)
c[j].flag = 1; // 标记为已选中
}
}
count = 0;
for (int i = 0; i < T; i++){
int x, y;
max.d = 0;
scanf("%d%d", &x, &y);
// 遍历第一组 n 个密码机,找到与当前询问坐标最远的密码机
for (int j = 0; j < n; j++){
c[j].d = far(x, y, c[j].x, c[j].y);
if (c[j].d > max.d){
max.d = c[j].d;
max.t = j; // 最远密码机的索引
max.id = c[j].id; // 最远密码机的id
}
}
// 判断最远密码机是否被标记
if (c[max.t].flag == 1)
count++;
}
printf("%d", count);
return 0;
}
第三天 7月19日:STL:vector(向量)、stack(栈)、queue(列队)
第一题:Problem B: 括弧匹配检验 (stack)
假设表达式中允许包含两种括号:圆括号和方括号,其嵌套的顺序随意,如 ([]())或 [([][])]等为正确的匹配,[(])或 ([]()或 (()))均为错误的匹配。
现在的问题是,要求检验一个给定表达式中的括弧是否正确匹配?
输入一个只包含圆括号和方括号的字符串,判断字符串中的括号是否匹配,匹配就输出 “OK” ,不匹配就输出“Wrong”。
输入一个字符串:[([][])],输出:OK
Input :输入仅一行字符(字符个数小于255)
Output:匹配就输出 “OK” ,不匹配就输出“Wrong”
#include <iostream>
#include <string>
#include <stack>
using namespace std;
bool isMatching(char left, char right) {
return (left == '(' && right == ')') || (left == '[' && right == ']');
}
int main() {
string s;
cin >> s;
stack<char> st;
for (char ch : s) {
if (ch == '(' || ch == '[') {
st.push(ch); // 如果遇到左括号 '(' 或 '[',则将其压入栈中
} else if (ch == ')' || ch == ']') {
if (st.empty() || !isMatching(st.top(), ch)) {
// 如果栈为空或栈顶的左括号与当前的右括号不匹配,输出"Wrong"
cout << "Wrong" << endl;
return 0; // 提前结束程序
}
st.pop(); // 弹出栈顶的左括号 '(' 或 '[',表示配对成功
}
}
if (st.empty()) {
cout << "OK" << endl; // 如果栈为空,说明所有括号都匹配成功,输出"OK"
} else {
cout << "Wrong" << endl;
}
return 0;
}
第二题:A - 狼人杀 (约瑟夫环问题)
大哲是一个忠实的狼人杀爱好者,而且是高手中的高手。由于她过于擅长各类套路,并且具备敏锐的直觉与极强的心理素质,甚至还是一个心理学博士,她的朋友逐渐失去了游戏体验。为了照顾她的朋友,她决定制定一种不靠计谋、不用推理,全靠强运的“杀法”: 游戏玩家围成一个圈,从指定的第一个人开始数数,数到第 m 个人时,那个人就会被处死。之后从被处死的人的后一个人开始数数,再数到第 m 个人处死......依此方法不断杀死玩家。假如说玩家有好人与坏人两种身份,每种身份各 n 人,试问如何安排这些人的座位,能使得在处死 n 人后,剩下的 n 人都是好人
Input:多组数据,每组数据输入:好人和坏人的人数n(<=32767)、步长m(<=32767);
Output:对于每一组数据,输出2n个大写字母,‘G’表示好人,‘B’表示坏人,50个字母为一行,不允许出现空白字符。相邻两组输出之间有一个空行隔开。
思路:因为要求剩下的n人都是好人,所以我们将所有人初始化为好人,被处死的人标记为坏人。
#include<stdio.h>
struct player{ //玩家信息的结构体
int id;
int flag;
char role;
}p[33000];
void check(int n,int m,struct player p[33000]);
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m)){
check(2*n,m,p);
for(int i=1;i<=2*n;i++) printf("%c",p[i].role);
printf("\n\n");
}
return 0;
}
void check(int n,int m,struct player p[33000])
{
for(int i=1;i<=n;i++){
p[i].flag=0;
p[i].id=i;
p[i].role='G'; //初始化为好人
}
int d=0,k=0,i=0;
while(d!=n/2){
i++;
if(i>n) i=1;
if(p[i].flag==0){
k++;
if(k==m){
p[i].role='B';//要被处死,标记为坏人
p[i].flag=1;
//printf("%d ",i);
d++;
k=0;
}
}
}
return;
}
第四天:7月20日:STL:deque(双端队列)、priority_queue(优先队列)、list(链表)、set(集合)、map(映射)、pair
第一题:I-看病要排队 (优先队列)
看病要排队这个是地球人都知道的常识。 不过经过细心的0068的观察,他发现了医院里排队还是有讲究的。0068所去的医院有三个医生(汗,这么少)同时看病。而看病的人病情有轻重,所以不能根据简单的先来先服务的原则。所以医院对每种病情规定了10种不同的优先级。级别为10的优先权最高,级别为1的优先权最低。医生在看病时,则会在他的队伍里面选择一个优先权最高的人进行诊治。如果遇到两个优先权一样的病人的话,则选择最早来排队的病人。 现在就请你帮助医院模拟这个看病过程。
Input
输入数据包含多组测试,请处理到文件结束。 每组数据第一行有一个正整数N(0<N<2000)表示发生事件的数目。 接下来有N行分别表示发生的事件。 一共有两种事件: 1:"IN A B",表示有一个拥有优先级B的病人要求医生A诊治。(0<A<=3,0<B<=10) 2:"OUT A",表示医生A进行了一次诊治,诊治完毕后,病人出院。(0<A<=3)
Output
对于每个"OUT A"事件,请在一行里面输出被诊治人的编号ID。如果该事件时无病人需要诊治,则输出"EMPTY"。 诊治人的编号ID的定义为:在一组测试中,"IN A B"事件发生第K次时,进来的病人ID即为K。从1开始编号。
思路:给每一个医生都建立一个优先队列
#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
using namespace std;
struct per
{
int num,id;
}s;
//先定义结构体,再写重载函数定义优先级比较简单明了
bool operator < (const per &x,const per &y)//重载 "<" 操作符定义优先级
{
if(x.num==y.num)//当级别相同时从小到大排序
return x.id>y.id;
else
return x.num<y.num;//当级别不同是从大到小排序
}
int main()
{
int n,a,b;
char str[5];
while(scanf("%d",&n)!=EOF)
{
int k=1;
priority_queue<per>q[4];
while(n--)
{
scanf("%s%d",str,&a);
if(strcmp(str,"IN")==0)
{
scanf("%d",&b);
s.num=b;
s.id=k++;//储存病人的ID;
q[a].push(s);//把病人入队列;
}
else
{
if(!q[a].empty())//有医生诊断
{
s=q[a].top();
q[a].pop();
printf("%d\n",s.id);
}
else
printf("EMPTY\n");
}
}
}
return 0;
}
第二题:H-士兵列队训练问题 (vector)
某部队进行新兵队列训练,将新兵从一开始按顺序依次编号,并排成一行横队,训练的规则如下:从头开始一至二报数,凡报到二的出列,剩下的向小序号方向靠拢,再从头开始进行一至三报数,凡报到三的出列,剩下的向小序号方向靠拢,继续从头开始进行一至二报数。。。。以后从头开始轮流进行一至二报数、一至三报数直到剩下的人数不超过三人为止。
Input:本题有多个测试数据组,第一行为组数,接着为行新兵人数,新兵人数不超过。
Output:共有行,分别对应输入的新兵人数,每行输出剩下的新兵最初的编号,编号之间有一个空格。
#include <iostream>
#include <vector>
using namespace std;
int main() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
vector<int> v;
for (int i = 1; i <= n; i++)
v.push_back(i); // 输入数据
while (v.size() > 3) {
int sum = v.size();
// 报到2的出列,总共要删 sum/2 个
for (int i = 1; i <= sum / 2; i++)
v.erase(v.begin() + i);
sum = v.size();
if (sum <= 3)
break;
// 模拟了第一轮报1~3的所有报到3的人
for (int i = 1; i <= sum / 3; i++)
v.erase(v.begin() + i * 2);
// 如果此时剩的人数比3要多,在进行下一轮报数
}
for (int i = 0; i < v.size(); i++) {
if (i == 0)
cout << v[i];
else
cout << ' ' << v[i];
}
cout << '\n';
}
return 0;
}
第三题:B - Ignatius and the Princess II (next_permutation函数)
Now our hero finds the door to the BEelzebub feng5166. He opens the door and finds feng5166 is about to kill our pretty Princess. But now the BEelzebub has to beat our hero first. feng5166 says, "I have three question for you, if you can work them out, I will release the Princess, or you will be my dinner, too." Ignatius says confidently, "OK, at last, I will save the Princess." "Now I will show you the first problem." feng5166 says, "Given a sequence of number 1 to N, we define that 1,2,3...N-1,N is the smallest sequence among all the sequence which can be composed with number 1 to N(each number can be and should be use only once in this problem). So it's easy to see the second smallest sequence is 1,2,3...N,N-1. Now I will give you two numbers, N and M. You should tell me the Mth smallest sequence which is composed with number 1 to N. It's easy, isn't is? Hahahahaha......" Can you help Ignatius to solve this problem?
Input
The input contains several test cases. Each test case consists of two numbers, N and M(1<=N<=1000, 1<=M<=10000). You may assume that there is always a sequence satisfied the BEelzebub's demand. The input is terminated by the end of file.
Output
For each test case, you only have to output the sequence satisfied the BEelzebub's demand. When output a sequence, you should print a space between two numbers, but do not output any spaces after the last number.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
int N, M;
while(cin >> N >> M){
if(N==0&&M==0) break;
vector<int> nums(N);
for (int i = 0; i < N; ++i)
nums[i] = i + 1;
for(int i=1; i<M;i++){
next_permutation(nums.begin(),nums.end());
}
for(int i=0;i<N;i++){
cout<<nums[i];
if(i!=N-1) cout<<" ";
}
cout<<endl;
}
return 0;
}