日常集训第二周周记(9月18号-9月24号)
部分题目详细分析与总结
第一题:蛇形填数1-顺时针填数
在方阵里填入,要求填成蛇形。例如时方阵为:
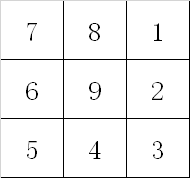
时方阵为:
输入格式:
输入正整数
输出格式:
按题目要求输出阶方阵,一共行,要求每个数占列,右对齐。
输入样例:
3
输出样例:
7 8 1
6 9 2
5 4 3
解题思路: 我们使用一个二维数组来表示这个方阵,然后用一个方向数组,存储上下左右四个方向,通过循环来遍历这个矩阵,每次遍历到一个位置,就把当前的数字赋值给这个位置,然后判断下一个位置是不是已经赋值过了,如果赋值过了,就改变方向,然后继续赋值,直到所有的位置都赋值完毕。
本题时间复杂度为
#include<bits/stdc++.h> //万能头文件
using namespace std;
int dir[][2] = {{1,0},{0,-1},{-1,0},{0,1}}; //四个移动方向
int a[30][30];
int main(){
int n;
cin >> n;
int r = 1,c = n, d = 0;
for(int i = 1; i<=n*n;i++){
a[r][c] = i;
int nr = r + dir[d][0];
int nc = c + dir[d][1];
if(nr < 1 || nr > n || nc < 1 || nc > n || a[nr][nc]){ //撞墙或者撞到自己(边界条件)
d = (d+1)%4; //拐弯
}
r += dir[d][0]; //移动
c += dir[d][1];
}
for(int i = 1; i<=n;i++){
for(int j = 1; j<=n;j++){
printf("%4d",a[i][j]); //%4d表示输出4位整数,不足4位的用空格补齐
}
cout << endl;
}
return 0;
}
第二题:过河(贪心)
有个人想要过一条河,但是他们只有一条最多载两人的船。因此必须想出一个调度船来回的方法让每个人都能过河。每个人都有自己的划船速度,且同一条船上的两个人取决于慢者的速度。你的任务就是想出一个每人都能过河的最快策略。
输入格式:
输入的第一行是一个正整数,表示测试用例的组数。下面是组用例。每个用例的第一行是正整数,第二行是个正整数表示每个人的划船速度。每组用例不会超出1000个人,每个人的划船时间不会超过秒。
输出格式:
对于每个用例,输出所有个人都能过河的最短时间(秒)。
输入样例:
2
3
1 3 7
4
1 2 5 10
输出样例:
11
17
解题思路: 本题是一个贪心问题,首先对所有要过河的人的划船速度按从快到慢排序,选择渡河时间最短的两个人作为船夫与,每次选择渡河时间最长的两个人作为与进行渡河,比较两种过河方案所花的时间,选择时间较短的那一个。 重复以上步骤,每次人过河,直到剩下小于四个人 如果剩下人,按渡河时间从小到大分别为,,,那么最佳的渡河方案为:与到对岸,回来,与到对岸,渡河时间为: 如果剩下2人,则,两人可以直接渡到对岸,渡河时间为。 如果剩下1人,那么渡河时间为。
本题时间复杂度为
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
int main()
{
int n, T, t[N];
cin >> T;
while(T--)
{
int sum = 0;
int i;
cin >> n;
for(i = 1; i <= n; ++i)
cin >> t[i];
sort(t+1,t+1+n); //排序
for(i = n; i >= 4; i-=2)
sum += min(2*t[1]+t[i]+t[i-1], t[1]+2*t[2]+t[i]); //最小的两个和最大的两个
if(i == 3)
sum += t[1]+t[2]+t[3];
else if(i == 2)
sum += t[2];
else
sum += t[1];
cout << sum << endl;
}
return 0;
}
第三题:321-like Searcher
A positive integer is called a 321-like Number when it satisfies the following condition. This definition is the same as the one in Problem .
- The digits of are strictly decreasing from top to bottom.
- In other words, if has d digits, it satisfies the following for every integer i such that :
- (the i-th digit from the top of ) > (the ()-th digit from the top of ).
Note that all one-digit positive integers are 321-like Numbers.
For example, , , and are 321-like Numbers, but ,, and are not.
Find the -th smallest 321-like Number.
输入格式: The input is given from Standard Input in the following format:
K
输出格式: Print the -th smallest 321-like Number as an integer.
输入样例1:
15
输出样例1:
32
The 321-like Numbers are from smallest to largest. The -th smallest of them is .
输入样例2:
321
输出样例2:
9610
输入样例3:
777
输出样例3:
983210
解题思路:
首先按照题的思路,我们将数字录入后将其拆解为单个数字,因为321型数字是从高位向低位递减的,但拆解时从低位开始,所以判断时,只要判断拆解后存放在数组中的数字,满足当前索引大于前一索引即可。因为本题要找的是从开始第个321型数,所以我们添加count变量,每次判断成功后count++,当count==K时,输出当前数字即可。
以下是我的代码:
#include <iostream>
using namespace std;
const int N = 1e5 + 5;
int main() {
int m;
cin >> m;
int count = 0;
int num = 1; // 从1开始逐个检查数字
while (count < m) {
int a[N];
int temp = num;
int len = 0;
while (temp > 0) {
a[len] = temp % 10;
temp /= 10;
len++;
}
int flag = 1; // 假设是 "321-型数字"
for (int i = 0; i < len - 1; i++) {
if (a[i] >= a[i + 1]) { // 如果有一对不满足条件的相邻数字
flag = 0; // 不是 "321-型数字"
break;
}
}
if (flag) {
count++; // 找到一个符合条件的数字
}
if (count < m) {
num++; // 继续检查下一个数字
}
}
cout << num << endl;
return 0;
}
但是这样做会在最后五个测试点超时,所以需要对代码进行优化。根据官方给的代码,思路是首先对所有321型数字生成进行打表,然后录入,查找表中对应的数字再输出即可,这样的时间复杂度只有
#include <bits/stdc++.h>
using namespace std;
int main()
{
vector<long long> v;
// 从2开始循环到 2^10 - 1,即 1023,因为最大的 321-型数字有10位
for (int i = 2; i < (1 << 10); i++)
{
long long x = 0;
// 从9到0逆向循环,检查二进制中的每一位是否为1
for (int j = 9; j >= 0; j--)
{
if (i & (1 << j)) // 使用位运算检查二进制位是否为1
{
x *= 10; // 将 x 左移一位,相当于在数字的末尾添加一个0
x += j; // 将 j 添加到 x 的末尾,构建当前的 321-型数字
}
}
v.push_back(x);
}
sort(v.begin(), v.end()); // 对存储的数字进行升序排序
int k;
cin >> k;
cout << v[k - 1] << endl;
return 0;
}