暑假集训第五篇周记(8月7日-8月13日)
摘要
涉及内容: 并查集、线段树、树状数组、递推算法
每日知识点
第一天8月7日:并查集
并查集是一种常用的数据结构,用于解决集合合并和查询问题。它主要支持两种操作:合并(Union)和查找(Find)。
并查集通常用于解决一些关于元素之间连通性和集合之间合并的问题。经典应用场景包括:
- 判断无向图中的两个节点是否连通。
- 管理不相交集合的合并和查询。
并查集的数据结构可以用一棵树来表示,其中每个节点代表一个元素,树的根节点表示集合的代表元素。每个节点都有一个指针指向其父节点,根节点没有父节点。通过这种方式,可以快速判断两个元素是否在同一个集合中。
并查集主要包含以下两个操作:
- 查找(Find):用于查找某个元素所属的集合,即找到其根节点。
- 合并(Union):用于合并两个元素所属的集合,即将一个元素的根节点指向另一个元素的根节点,从而将两个集合合并成一个集合。
通过这两个操作,我们可以快速实现集合合并和查询的功能,用于解决各种连通性和集合合并问题。
并查集的实现有多种方法,其中一种常用的实现方式是使用数组来表示树的结构,并通过路径压缩和按秩合并等优化技术来提高查找和合并的效率。
第二天8月8日:线段树(Segment Tree)
线段树(Segment Tree) 是一种在处理区间查询和修改问题时非常有用的数据结构。它可以在对数时间内完成区间操作,通常用于解决需要在一维或多维区间上进行查询和更新的问题。线段树的核心思想是将待处理的区间划分成一系列的小区间,然后通过构建一棵树来表示这些小区间,从而使得查询和修改操作可以高效地进行。
线段树主要用于解决以下两种类型的问题:
- 区间查询问题:给定一个区间 [L, R],需要在这个区间上执行某种操作(例如求和、最大值、最小值等)并返回结果。这种查询可以在对数时间内完成,因为线段树的结构能够使我们有效地定位到涉及的子区间。
- 区间修改问题:给定一个区间 [L, R],需要对这个区间内的元素执行某种修改操作(例如增加、赋值等)。线段树可以高效地处理这种修改,同时确保不必每次都更新整个区间。
线段树的构建和操作需要经过以下步骤:
- 构建树:构建一棵表示整个区间的树,树的每个节点代表一个区间范围,根节点表示整个区间,子节点分别表示其一半的区间。
#define lc p << 1 //左孩子编号为父节点编号*2
#define rc p << 1 | 1 //右孩子编号为父节点编号*2+1
const int N = 1e5 + 5;
int n,w[N];
struct node{
int l,r,sum; //左节点、右节点、和
}tr[N*4];
void build(int p, int l, int r){ //访问的根节点p,左子节点l,右子节点r
tr[p] = {l,r,w[1]}; //初始化
if(l == r) return; //如果左端点=右端点,即到达叶子节点,无法分裂,退出
int m = (1 + r) >> 1; //不是叶子节点,就裂开
build(lc,l,m); //递归
build(rc,m+1,r);
tr[p].sum = tr[lc].sum + tr[rc].sum; //父节点的和为子节点和
}
查询操作:从树的根节点开始,根据查询的区间范围,递归地向下搜索,找到涉及的叶节点区间并返回所需的结果。拆分和拼凑的思想。
从根节点进入,递归执行以下过程:
- 若查询区间完全覆盖当前节点区间,则立即回溯,并返回该节点值
- 若区间左子节点与有重叠,则递归访问左子树
- 若区间右子节点与有重叠,则递归访问右子树
int query(int p, int x, int y){ //区间查询,x y分别为查询区域左右端点
if(x <= tr[p].l && tr[p].r <= y) //如果覆盖则返回
return tr[p].sum;
int m = (tr[p].l + tr[p].r) >> 1; //如果不覆盖就裂开
int sum = 0;
if(x <= m) sum += query(lc,x,y);
if(y > m) sum += query(rc,x,y);
return sum;
}
更新操作:从树的根节点开始,根据更新的区间范围,递归地向下搜索,更新涉及的节点,并确保更新的值被正确地传递到父节点。
分为点修改和区间修改两种类型
点修改:从根节点进入,递归找到叶子节点,把该节点的值增加k,然后从下往上更新其祖先节点的统计值
void update(int p, int x, int k){
if(tr[p].l == x && tr[p].r == x){
tr[p].sum += k;
return;
}
int m = (tr[p].l + tr[p].r) >> 1;
if(x <= m) update(lc,x,k);
if(x > m) update(rc,x,k);
tr[p].sum = tr[lc].sum + tr[rc].sum;
}
区间修改:采用懒惰修改,当完全覆盖节点区间时,先修改该区间的sum值,再打上一个Lazy-Tag,然后立即返回。 Lazy Tag 可以有效地处理多次区间修改操作,同时在需要真正访问区间值时才进行计算,避免了不必要的计算开销。 在一些问题中,可能需要对区间进行多次修改,如果每次都立即更新整个区间,会导致重复计算,从而效率较低。Lazy Tag 的核心思想是将修改操作推迟到真正需要获取区间值时进行,将修改标记(Lazy Tag)存储在树的节点中,以表示该节点所代表的区间内的值需要更新。当需要获取某个区间的值时,Lazy Tag 会递归地将标记向下传递,直到达到叶子节点或需要真正计算的节点,然后在计算时再进行实际的修改操作。
Lazy Tag 主要包括以下步骤:
- 在树的节点中添加标记:对于每个节点,添加一个表示修改标记的变量。当需要修改某个区间时,只需要将标记添加到该区间的根节点。
- 标记的传递:在进行查询或获取区间值的操作时,递归地将标记从父节点传递到子节点,直到达到叶子节点或需要计算的节点。
- 实际的修改操作:当需要计算区间值时,根据标记的传递情况,在需要计算的节点上进行真正的修改操作,然后将标记清除。
此时,结构体需要添加一个int类型的add变量,表示Lazy-Tag
void pushup(int p) { //向上更新
s[p].sum = s[lc].sum + s[rc].sum;
}
void pushdown(int p) { //向下更新
if (s[p].add) {
s[lc].sum += tr[p].add*(tr[lc].r - tr[lc].l + 1),
s[rc].sum += tr[p].add*(tr[rc].r - tr[rc].l + 1),
s[lc].add += tr[p].add,
s[rc].add += tr[p].add,
s[p].add = 0;
}
}
void update(int p, int x, int y) {
if (x <= s[p].l && s[p].r <= y) {
tr[p].sum += (tr[p].r - tr[p].l + 1) *k;
tr[p].add += k;
return;
}
int m = (s[p].l + s[p].r) >> 1;
pushdown(p);
if (x <= m) update(lc, x, y);
if (y > m) update(rc, x, y);
pushup(p);
}
第三天8月9日:线段树(Segment Tree)
内容同第二天
第四天8月10日:树状数组(Binary Indexed Tree,BIT )
树状数组是一种支持 单点修改 和 区间查询 的,代码量小的数据结构,是利用数的二进制特征进行检索的一种树状结构。
下图展示了树状数组的工作原理:
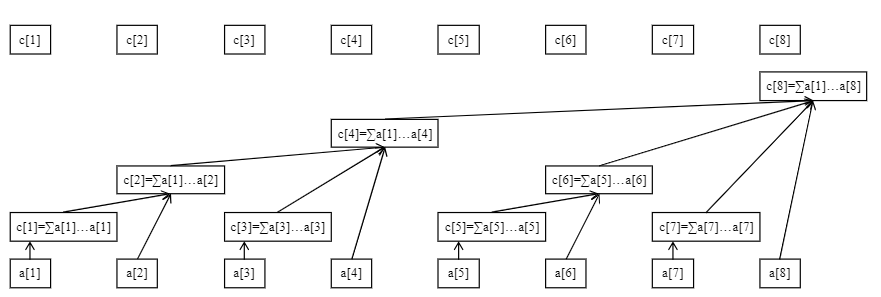
最下面的八个方块代表原始数组。上面参差不齐的方块(与最上面的八个方块是同一个数组)代表数组的上级——数组
数组是用来储存原始数组某段区间和的,也就是说,这些区间的信息是已知的,我们的目标就是把查询前缀拆成这些小区间。
例如,从图中可以看出:
- 管辖的是
- 管辖的是
- 管辖的是
- 管辖的是
- 剩下的管辖的都是自己,(可以看做的长度为1的小区间)
管辖区间
树状数组中,规定管辖的区间长度为,其中:
- 设二进制最低位为第位,则 恰好为 二进制表示中,最低位的
1所在的二进制位数 - (的管辖区间长度) 恰好为 二进制表示中,最低位的
1以及后面所有0组成的数
我们记二进制最低位 1以及后面的 0组成的数为,那么管辖的区间就是
根据位运算,我们用 lowbit(x) = x & -x来计算
//两种定义方式:
#define lowbit(x) ((x) & -(x))
int lowbit(int x){
return x & -x;
}
区间查询
当我们查询前缀和的过程:
从往前跳,发现只管辖这个元素;然后找到,发现管辖的是,然后跳到了管辖的是这些元素,然后再试图跳到,但实际上不存在,就不跳了。最后把这些都加起来。
由上面的过程,每次往前跳,一定是跳到现区间的左端点的左一位,作为新区见的右端点,这样才能将前缀不重不漏地拆分。
以下是查询的过程:
- 从开始往前跳,有管辖
- 令,如果 说明已经跳到尽头了,终止循环;否则回到第一步。
- 将跳到的合并。
int getsum(int x) { // a[1]..a[x]的和
int ans = 0;
while (x > 0) {
ans = ans + c[x];
x = x - lowbit(x);
}
return ans;
}
单点修改
设表示的大小,以下是单点修改的过程:
- 初始令
- 修改
- 令 + ,如果 说明已经跳到尽头了,终止循环;否则回到第二步。
void add(int x, int k) {
while (x <= n) { // 不能越界
c[x] = c[x] + k;
x = x + lowbit(x);
}
}
二维树状数组
子矩阵加,求子矩阵和
typedef long long ll;
ll t1[N][N], t2[N][N], t3[N][N], t4[N][N];
void add(ll x, ll y, ll z) {
for (int X = x; X <= n; X += lowbit(X))
for (int Y = y; Y <= m; Y += lowbit(Y)) {
t1[X][Y] += z;
t2[X][Y] += z * x; // 注意是 z * x 而不是 z * X,后面同理
t3[X][Y] += z * y;
t4[X][Y] += z * x * y;
}
}
void range_add(ll xa, ll ya, ll xb, ll yb,
ll z) { //(xa, ya) 到 (xb, yb) 子矩阵
add(xa, ya, z);
add(xa, yb + 1, -z);
add(xb + 1, ya, -z);
add(xb + 1, yb + 1, z);
}
ll ask(ll x, ll y) {
ll res = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
res += (x + 1) * (y + 1) * t1[i][j] - (y + 1) * t2[i][j] -
(x + 1) * t3[i][j] + t4[i][j];
return res;
}
ll range_ask(ll xa, ll ya, ll xb, ll yb) {
return ask(xb, yb) - ask(xb, ya - 1) - ask(xa - 1, yb) + ask(xa - 1, ya - 1);
}
第五天8月11日:递推算法
递推算法是一种通过已知的初始条件和前一项的计算结果,来逐步推导出后续项的方法。在数学、计算机科学和其他领域中,递推算法被广泛用于解决各种问题,从生成数列到求解动态规划问题都可以使用递推方法。
递推算法通常分为两种类型:线性递推和递归递推。
- 线性递推: 线性递推是一种基于迭代的方法,其中每一项都是根据前面的一些项计算得出的。最常见的例子就是斐波那契数列,其中每一项都是前两项之和。线性递推的计算通常基于一些公式或规律,而不涉及递归调用。这种方法通常比较高效,因为避免了递归调用的开销。
- 递归递推: 递归递推是一种通过将问题分解为更小的相似子问题,然后通过递归调用来解决的方法。在递归递推中,问题的求解依赖于较小规模的同类型问题的解。典型的例子是阶乘计算,其中 n! 可以通过 (n-1)! 计算得出。虽然递归递推可能更直观,但在实际应用中可能会引入较大的计算开销,尤其是在递归深度较大时。
部分题目详细分析与总结
第一天8月7日:并查集
第一题:并查集(模板)
如题,现在有一个并查集,你需要完成合并和查询操作。
Input
第一行包含两个整数 ,表示共有 个元素和 个操作。
接下来 行,每行包含三个整数 。
当 时,将 与 所在的集合合并。
当 时,输出 与 是否在同一集合内,是的输出 Y ;否则输出 N 。
Output
对于每一个 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
Sample
Input Output
4 7 N
2 1 2 Y
1 1 2 N
2 1 2 Y
1 3 4
2 1 4
1 2 3
2 1 4
对于 的数据,,。
对于 的数据,,。
对于 的数据,,,,。
代码
#include <iostream>
using namespace std;
const int N = 1e4 + 5; // 定义一个常量 N,表示数组的最大大小
int n, m, x, y; // 输入的人数 n,操作次数 m,操作中涉及的两个人的编号 x 和 y
int a[N]; // 数组 a 用于存储并查集的根节点
// 并查集的查找操作,寻找元素 k 的根节点
int find(int k) {
if (k != a[k]) a[k] = find(a[k]); // 路径压缩,将当前元素的根节点更新为最终的根节点
return a[k];
}
int main() {
cin >> n >> m; // 输入人数 n 和操作次数 m
// 初始化并查集,初始时每个人的根节点就是自己
for (int i = 1; i <= n; i++) {
a[i] = i;
}
int z; // 操作类型,1 表示合并操作,2 表示查询操作
for (int i = 1; i <= m; i++) {
cin >> z >> x >> y; // 输入操作类型和涉及的两个人的编号
if (z == 1) // 如果操作是合并操作
a[find(x)] = find(y); // 将 x 的根节点连接到 y 的根节点上
else {
if (find(x) == find(y)) // 如果 x 和 y 的根节点相同,说明它们在同一个集合中
cout << "Y" << endl; // 输出 "Y" 表示在同一个集合
else
cout << "N" << endl; // 否则输出 "N" 表示不在同一个集合
}
}
return 0;
}
第二题:朋友
小明在 A 公司工作,小红在 B 公司工作。
这两个公司的员工有一个特点:一个公司的员工都是同性。
A 公司有 名员工,其中有 对朋友关系。B 公司有 名员工,其中有 对朋友关系。朋友的朋友一定还是朋友。
每对朋友关系用两个整数 组成,表示朋友的编号分别为 。男人的编号是正数,女人的编号是负数。小明的编号是 ,小红的编号是 。
大家都知道,小明和小红是朋友,那么,请你写一个程序求出两公司之间,通过小明和小红认识的人最多一共能配成多少对情侣(包括他们自己)。
Input
输入的第一行,包含 个空格隔开的正整数 。
之后 行,每行两个正整数 。
之后 行,每行两个负整数 。
Output
输出一行一个正整数,表示通过小明和小红认识的人最多一共能配成多少对情侣(包括他们自己)。
Sample
Input Output
4 3 4 2 2
1 1
1 2
2 3
1 3
-1 -2
-3 -3
对于 的数据,,;
对于 的数据,,;
对于 的数据,,。
代码
#include<bits/stdc++.h>
#define r(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
int n, m, p, q, u, v, tat, tot;
map<int, int> f; // 使用 STL 中的 map 容器来实现并查集
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]); // 路径压缩
}
void judge(int x, int y) {
f[find(x)] = find(y); // 合并两个元素的集合
}
bool too(int x, int y) {
return find(x) == find(y); // 判断两个元素是否在同一集合中
}
int main() {
scanf("%d%d%d%d", &n, &m, &p, &q); // 输入 n, m, p, q
r(i, -1 * m, n) f[i] = i; // 初始化并查集,每个元素自成一个集合
r(i, 1, p + q) {
scanf("%d%d", &u, &v); // 读入朋友关系
judge(u, v); // 合并朋友关系中的两个元素所在的集合
}
r(i, -1 * m, -1)
if (too(f[i], -1)) tat++; // 找连接在一起的和小红的朋友
r(i, 1, n)
if (too(f[i], 1)) tot++; // 找连接在一起的和小明的朋友
printf("%d", min(tat, tot)); // 输出两者之间较小的值,即最多能配对多少对情侣
return 0;
}
第二天/第三天 8月8日/8月9日:线段树(Segment Tree)
第一题:线段树 1(模板)
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 。
- 求出某区间每一个数的和。
Input
第一行包含两个整数 ,分别表示该数列数字的个数和操作的总个数。
第二行包含 个用空格分隔的整数,其中第 个数字表示数列第 项的初始值。
接下来 行每行包含 或 个整数,表示一个操作,具体如下:
1 x y k:将区间 内每个数加上 。2 x y:输出区间 内每个数的和。
Output
输出包含若干行整数,即为所有操作 2 的结果。
Sample
Input Output
5 5 11
1 5 4 2 3 8
2 2 4 20
1 2 3 2
2 3 4
1 1 5 1
2 1 4
对于 的数据:,。 对于 的数据:,。 对于 的数据:。
保证任意时刻数列中所有元素的绝对值之和 。
代码
#include <cstdio>
#define MAXN 1000001
#define ll long long
using namespace std;
unsigned ll n, m, a[MAXN], ans[MAXN << 2], tag[MAXN << 2];
// 左子节点的下标
inline ll ls(ll x) {
return x << 1;
}
// 右子节点的下标
inline ll rs(ll x) {
return x << 1 | 1;
}
// 输入函数,读取 n、m 和数组 a
void scan() {
scanf("%llu%llu", &n, &m);
for (ll i = 1; i <= n; i++)
scanf("%lld", &a[i]);
}
// 更新父节点的值
inline void push_up(ll p) {
ans[p] = ans[ls(p)] + ans[rs(p)];
}
// 递归建立线段树
void build(ll p, ll l, ll r) {
tag[p] = 0;
if (l == r) {
ans[p] = a[l]; // 叶节点存储数组中的元素
return;
}
ll mid = (l + r) >> 1;
build(ls(p), l, mid); // 递归建立左子树
build(rs(p), mid + 1, r); // 递归建立右子树
push_up(p); // 更新当前节点的值
}
// 增加父节点的标记值
inline void f(ll p, ll l, ll r, ll k) {
tag[p] = tag[p] + k;
ans[p] = ans[p] + k * (r - l + 1);
}
// 将父节点的标记值向下传递给子节点
inline void push_down(ll p, ll l, ll r) {
ll mid = (l + r) >> 1;
f(ls(p), l, mid, tag[p]);
f(rs(p), mid + 1, r, tag[p]);
tag[p] = 0;
}
// 区间更新操作
inline void update(ll nl, ll nr, ll l, ll r, ll p, ll k) {
if (nl <= l && r <= nr) { // 如果当前区间被包含在查询区间中
ans[p] += k * (r - l + 1); // 更新当前节点的值
tag[p] += k; // 增加当前节点的标记值
return;
}
push_down(p, l, r); // 将标记值向下传递
ll mid = (l + r) >> 1;
if (nl <= mid) update(nl, nr, l, mid, ls(p), k); // 更新左子树
if (nr > mid) update(nl, nr, mid + 1, r, rs(p), k); // 更新右子树
push_up(p); // 更新当前节点的值
}
// 区间查询操作
ll query(ll q_x, ll q_y, ll l, ll r, ll p) {
ll res = 0;
if (q_x <= l && r <= q_y) // 如果当前区间被包含在查询区间中
return ans[p]; // 直接返回当前节点的值
ll mid = (l + r) >> 1;
push_down(p, l, r); // 将标记值向下传递
if (q_x <= mid) res += query(q_x, q_y, l, mid, ls(p)); // 查询左子树
if (q_y > mid) res += query(q_x, q_y, mid + 1, r, rs(p)); // 查询右子树
return res;
}
int main() {
ll a1, b, c, d, e, f;
scan();
build(1, 1, n); // 建立线段树
while (m--) {
scanf("%lld", &a1);
switch (a1) {
case 1: {
scanf("%lld%lld%lld", &b, &c, &d);
update(b, c, 1, n, 1, d); // 区间更新操作
break;
}
case 2: {
scanf("%lld%lld", &e, &f);
printf("%lld\n", query(e, f, 1, n, 1)); // 区间查询操作
break;
}
}
}
return 0;
}
第二题:敌兵布阵 (单点修改 + 区间查询)
C国的死对头A国这段时间正在进行军事演习,所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段,所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动,可能增加或减少若干人手,但这些都逃不过C国的监视。 中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动,而Derek每次询问的段都不一样,所以Tidy不得不每次都一个一个营地的去数,很快就精疲力尽了,Derek对Tidy的计算速度越来越不满:"你个死肥仔,算得这么慢,我炒你鱿鱼!”Tidy想:“你自己来算算看,这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下,Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说:“死肥仔,叫你平时做多点acm题和看多点算法书,现在尝到苦果了吧!”Tidy说:"我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼,这么算他真的会崩溃的,聪明的读者,你能写个程序帮他完成这项工作吗?不过如果你的程序效率不够高的话,Tidy还是会受到Derek的责骂的.
Input
第一行一个整数T,表示有T组数据。 每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。 接下来每行有一条命令,命令有4种形式: (1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30) (2)Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30); (3)Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数; (4)End 表示结束,这条命令在每组数据最后出现; 每组数据最多有40000条命令
Output
对第i组数据,首先输出“Case i:”和回车, 对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
Sample
Input Output
1 Case 1:
10 6
1 2 3 4 5 6 7 8 9 10 33
Query 1 3 59
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
代码
#include <cstdio>
using namespace std;
#define lc p << 1 //左孩子编号为父节点编号*2
#define rc p << 1 | 1 //右孩子编号为父节点编号*2+1
const int N = 1e5 + 5;
int w[N];
struct node{
int l,r,sum; //左节点、右节点、和
}tr[N*4];
void build(int p, int l, int r){ //建构线段树
tr[p] = {l,r,w[l]};
if(l == r) return;
int m = (l + r) >> 1;
build(lc,l,m);
build(rc,m+1,r);
tr[p].sum = tr[lc].sum + tr[rc].sum;
}
int query(int p, int x, int y){ //区间查询
if(x <= tr[p].l && tr[p].r <= y)
return tr[p].sum;
int m = (tr[p].l + tr[p].r) >> 1;
int sum = 0;
if(x <= m) sum += query(lc,x,y);
if(y > m) sum += query(rc,x,y);
return sum;
}
void update(int p, int x, int k){ //单点修改
if(tr[p].l == x && tr[p].r == x){
tr[p].sum += k;
return;
}
int m = (tr[p].l + tr[p].r) >> 1;
if(x <= m) update(lc,x,k);
if(x > m) update(rc,x,k);
tr[p].sum = tr[lc].sum + tr[rc].sum;
}
int main() {
int T;
scanf("%d", &T);
for (int tc = 1; tc <= T; ++tc) {
printf("Case %d:\n", tc);
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &w[i]);
}
build(1, 1, n);
char s[10]; // 使用字符数组来读取操作类型
int x, y, j;
while (scanf("%s", s) != EOF) { //读取操作,进行对应修改和输出
if (s[0] == 'E') break;
if (s[0] == 'Q') {
scanf("%d%d", &x, &y);
printf("%d\n", query(1, x, y));
} else if (s[0] == 'A') {
scanf("%d%d", &x, &j);
update(1, x, j);
} else {
scanf("%d%d", &x, &j);
update(1, x, -j);
}
}
}
return 0;
}
第三题:Just a Hook (区间修改 + 区间查询)
In the game of DotA, Pudge’s meat hook is actually the most horrible thing for most of the heroes. The hook is made up of several consecutive metallic sticks which are of the same length.
Now Pudge wants to do some operations on the hook. Let us number the consecutive metallic sticks of the hook from 1 to N. For each operation, Pudge can change the consecutive metallic sticks, numbered from X to Y, into cupreous sticks, silver sticks or golden sticks. The total value of the hook is calculated as the sum of values of N metallic sticks. More precisely, the value for each kind of stick is calculated as follows: For each cupreous stick, the value is 1. For each silver stick, the value is 2. For each golden stick, the value is 3. Pudge wants to know the total value of the hook after performing the operations. You may consider the original hook is made up of cupreous sticks.
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases. For each case, the first line contains an integer N, 1<=N<=100,000, which is the number of the sticks of Pudge’s meat hook and the second line contains an integer Q, 0<=Q<=100,000, which is the number of the operations. Next Q lines, each line contains three integers X, Y, 1<=X<=Y<=N, Z, 1<=Z<=3, which defines an operation: change the sticks numbered from X to Y into the metal kind Z, where Z=1 represents the cupreous kind, Z=2 represents the silver kind and Z=3 represents the golden kind.
Output
For each case, print a number in a line representing the total value of the hook after the operations. Use the format in the example.
Sample
Input Output
1 Case 1: The total value of the hook is 24.
10
2
1 5 2
5 9 3
代码
#include <cstdio>
#define lc p << 1 // 左孩子节点下标
#define rc p << 1 | 1 // 右孩子节点下标
const int N = 1e5 + 5; // 最大数组大小
int w[N]; // 原始数组 w,记录每个元素的初始值
struct node {
int l, r, sum, add; // 节点的左边界、右边界、和、懒惰标记(add 表示区间内元素被加上的值)
} tr[N * 4]; // 线段树的数组表示
void pushup(int p) { // 更新父节点的和
tr[p].sum = tr[lc].sum + tr[rc].sum;
}
void build(int p, int l, int r) {
tr[p] = {l, r, w[l], 0}; // 初始化节点为 [l, r] 区间的和为 w[l],懒惰标记为 0
if (l == r) return; // 叶节点,无需继续分裂
int m = (l + r) >> 1; // 计算中间点
build(lc, l, m); // 递归构建左子树
build(rc, m + 1, r); // 递归构建右子树
pushup(p); // 更新当前节点的和
}
void pushdown(int p) { // 将懒惰标记向下传递
if (tr[p].add) {
tr[lc].sum = tr[p].add * (tr[lc].r - tr[lc].l + 1); // 更新左子节点的和
tr[rc].sum = tr[p].add * (tr[rc].r - tr[rc].l + 1); // 更新右子节点的和
tr[lc].add = tr[p].add; // 更新左子节点的懒惰标记
tr[rc].add = tr[p].add; // 更新右子节点的懒惰标记
tr[p].add = 0; // 清空当前节点的懒惰标记
}
}
void update(int p, int x, int y, int k) { // 区间修改操作
if (x <= tr[p].l && tr[p].r <= y) { // 如果当前节点表示的区间完全包含在待修改的区间内
tr[p].sum = (tr[p].r - tr[p].l + 1) * k; // 更新当前节点的和
tr[p].add = k; // 设置当前节点的懒惰标记
return;
}
int m = (tr[p].l + tr[p].r) >> 1; // 计算当前节点的中间点
pushdown(p); // 将懒惰标记向下传递
if (x <= m) update(lc, x, y, k); // 递归更新左子树
if (y > m) update(rc, x, y, k); // 递归更新右子树
pushup(p); // 更新当前节点的和
}
int main() {
int T;
scanf("%d", &T); // 输入测试案例数
for (int i = 1; i <= T; i++) {
int n;
scanf("%d", &n); // 输入数组大小
getchar(); // 吸收换行符
for (int i = 1; i <= n; i++) {
w[i] = 1; // 初始化原始数组的元素为 1
}
build(1, 1, n); // 构建线段树
int q;
scanf("%d", &q); // 输入查询次数
for (int i = 1; i <= q; i++) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z); // 输入查询或修改操作的参数
update(1, x, y, z); // 执行区间修改操作
}
printf("Case %d: The total value of the hook is %d.\n", i, tr[1].sum); // 输出结果
}
return 0;
}
第四天8月10日:树状数组(Binary Indexed Tree, BIT)
第一题:康托展开(模板)
求 的一个给定全排列在所有 全排列中的排名。结果对 取模。
Input
第一行一个正整数 。
第二行 个正整数,表示 的一种全排列。
Output
一行一个非负整数,表示答案对 取模的值。
Sample 1
Input Output
3 3
2 1 3
Sample 2
Input Output
4 2
1 2 4 3
对于数据,。
对于数据,。
对于数据,。
代码
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll; // 定义长整型
ll tree[1000005]; // 树状数组
int n; // 数组的大小
// 计算 x 的二进制表示中的最低位 1 所代表的值
int lowbit(int x){
return x & -x;
}
// 树状数组的更新操作,在位置 x 加上值 y
void update(int x, int y){
while(x <= n){
tree[x] += y; // 在位置 x 加上 y
x += lowbit(x); // 更新下一个需要更新的位置
}
}
// 树状数组的查询操作,查询前 x 个位置的和
ll query(int x){
ll sum = 0;
while(x){
sum += tree[x]; // 累加前 x 个位置的值
x -= lowbit(x); // 向前移动,继续累加之前的位置
}
return sum;
}
const ll mod = 998244353; // 取模数
ll jc[1000005] = {1, 1}; // 存储阶乘的数组
int a[1000005]; // 存储输入的数
int main(){
scanf("%d", &n); // 输入数组的大小
// 预处理阶乘数组和初始化树状数组
for(int i = 1; i <= n; i++){
jc[i] = (jc[i - 1] * i) % mod; // 计算阶乘
update(i, 1); // 初始化树状数组
}
ll ans = 0; // 存储最终答案
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]); // 输入数组元素
// 计算当前位置的贡献,并累加到答案中
ans = (ans + ((query(a[i]) - 1) * jc[n - i]) % mod) % mod;
// 更新树状数组,将当前位置的值减一
update(a[i], -1);
}
printf("%lld", (ans + 1 + mod) % mod); // 输出最终答案,注意要保证答案为正数
return 0;
}
第五天8月11日:递推算法
第一题:数楼梯
楼梯有 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
Input:一个数字,楼梯数。
Output:输出走的方式总数。
Sample
Input Output
4 5
- 对于 的数据,;
- 对于 的数据,。
代码
#include <bits/stdc++.h>
using namespace std;
int n,len=1,f[5003][2000];//f[k][i]--第k阶台阶所对应的走法数
void step(int k)//高精度加法,k来存阶数
{
int i;
for(i=1;i<=len;i++)
f[k][i]=f[k-1][i]+f[k-2][i];//套用公式
for(i=1;i<=len;i++) //进位
if(f[k][i]>=10)
{
f[k][i+1]+=f[k][i]/10;
f[k][i]=f[k][i]%10;
if(f[k][len+1])len++;
}
}
int main()
{
scanf("%d",&n);
f[1][1]=1; f[2][1]=2; //初始化
for(int i=3;i<=n;i++) //从3开始避免越界
step(i);
for(int i=len;i>=1;i--) //逆序输出
printf("%d",f[n][i]);
return 0;
}