暑假集训第四篇周记（7月31日-8月6日）

岁杪二四...大约 21 分钟

摘要

涉及内容:贪心算法、二叉树、深搜（DFS）、宽搜（BFS）、堆

阿里巴巴走进了装满宝藏的藏宝洞。藏宝洞里面有 $N(N \le 100)$ 堆金币，第 $i$ 堆金币的总重量和总价值分别是 $m_i,v_i(1\le m_i,v_i \le 100)$ 。阿里巴巴有一个承重量为 $T(T \le 1000)$ 的背包，但并不一定有办法将全部的金币都装进去。他想装走尽可能多价值的金币。所有金币都可以随意分割，分割完的金币重量价值比（也就是单位价格）不变。请问阿里巴巴最多可以拿走多少价值的金币？

Input

第一行两个整数 $N,T$ 。

接下来 $N$ 行，每行两个整数 $m_i,v_i$ 。

Output

一个实数表示答案，输出两位小数

Sample

Input           Output
4 50            240.00
10 60
20 100
30 120
15 45

代码

#include <iostream>
#include <algorithm>

using namespace std;

struct bag {
    float w, v;   //重量和价值
};

bool cmp(bag c, bag d) {
    return (c.v / c.w) > (d.v / d.w);   //自定义一个结构体排序的函数
}

int main() {
    int N, T;    //N堆金币，T的背包重量
    cin >> N >> T;
    bag b[105];
    for (int i = 0; i < N; i++) {
        cin >> b[i].w >> b[i].v;
    }
    sort(b, b + N, cmp);
    float sum = 0.0;
    float weight_s = 0.0;
    for (int i = 0; i < N; i++) {
        if (weight_s + b[i].w <= T) {
            sum += b[i].v;
            weight_s += b[i].w;
        } else {
            // 当前物品不能完整装入背包，只装入能够容纳的部分
            float remaining_weight = T - weight_s;
            sum += (b[i].v / b[i].w) * remaining_weight;
            break;
        }
    }
    printf("%.2f", sum);
    return 0;
}

提示

所有物品的排序，是按照物品的单位价值从大到小排序的，这样的选择才是最优的。贪心算法中，需要每步选择最优的，以局部最优达到整体最优

第二天8月1日：二叉树、深搜、宽搜、堆

第一题：[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 $n-1$ 次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 $1$ ，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 $3$ 种果子，数目依次为 $1$ ， $2$ ， $9$ 。可以先将 $1$ 、 $2$ 堆合并，新堆数目为 $3$ ，耗费体力为 $3$ 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 $12$ ，耗费体力为 $12$ 。所以多多总共耗费体力 $=3+12=15$ 。可以证明 $15$ 为最小的体力耗费值。

Input

共两行。第一行是一个整数 $n(1\leq n\leq 10000)$ ，表示果子的种类数。

第二行包含 $n$ 个整数，用空格分隔，第 $i$ 个整数 $a_i(1\leq a_i\leq 20000)$ 是第 $i$ 种果子的数目。

Output

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 $2^{31}$ 。

Sample

Input        Output
3            15
1 2 9

提示

对于 $30\%$ 的数据，保证有 $n \le 1000$ ：

对于 $50\%$ 的数据，保证有 $n \le 5000$ ；

对于全部的数据，保证有 $n \le 10000$ 。

代码

#include <iostream>
#include <queue>
using namespace std;

int main() {
    // 创建一个最小堆优先队列，用于存储果子堆的大小
    priority_queue<int, vector<int>, greater<int>> pq;

    int n;
    cin >> n; // n 堆果子
    while (n--) {
        int x;
        cin >> x;
        pq.push(x); // 将每堆果子大小加入优先队列中
    }

    int energy = 0; // 表示当前合并的两堆果子的能量值
    int sum = 0; // 表示合并所有果子的总能量值

    // 当优先队列中还有多于一堆果子时，继续合并
    while (pq.size() > 1) {
        int a = pq.top(); // 取出当前最小的一堆果子
        pq.pop();
        int b = pq.top(); // 取出次小的一堆果子
        pq.pop();

        energy = a + b; // 合并两堆果子得到的能量值
        pq.push(energy); // 将能量值加入优先队列，表示合并后的果子堆
        sum += energy; // 累计总能量值
    }

    cout << sum << endl; // 输出最终合并所有果子的总能量值
    return 0;
}

第二题：堆（模板）

给定一个数列，初始为空，请支持下面三种操作：

给定一个整数 $x$ ，请将 $x$ 加入到数列中。
输出数列中最小的数。
删除数列中最小的数（如果有多个数最小，只删除 $1$ 个）。

Input

第一行是一个整数，表示操作的次数 $n$ 。接下来 $n$ 行，每行表示一次操作。每行首先有一个整数 $op$ 表示操作类型。

若 $op = 1$ ，则后面有一个整数 $x$ ，表示要将 $x$ 加入数列。
若 $op = 2$ ，则表示要求输出数列中的最小数。
若 $op = 3$ ，则表示删除数列中的最小数。如果有多个数最小，只删除 $1$ 个。

Output 对于每个操作 $2$ ，输出一行一个整数表示答案。

Sample

Input        Output
5            2
1 2          5
1 5
2
3
2

对于 $30\%$ 的数据，保证 $n \leq 15$ 。
对于 $70\%$ 的数据，保证 $n \leq 10^4$ 。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 10^6$ ， $1 \leq x \lt 2^{31}$ ， $op \in \{1, 2, 3\}$ 。

#include <bits/stdc++.h>
using namespace std;

priority_queue<int, vector<int>, greater<int>> q;

int main() {
    int n;
    scanf("%d", &n); // 输入操作次数

    while (n--) {
        int op;
        scanf("%d", &op); // 输入操作类型

        if (op == 1) {
            int x;
            scanf("%d", &x); // 输入要插入的元素 x
            q.push(x); // 将 x 加入优先队列中
        } else if (op == 2) {
            printf("%d\n", q.top()); // 输出当前优先队列中最小的元素
        } else {
            q.pop(); // 移除当前优先队列中最小的元素
        }
    }

    return 0;
}

第三天8月2日：深度优先搜索（Depth-First-Search,DFS）

第一题 N皇后问题（模板题、经典）

在 $N*N$ 的棋盘上放置N个皇后 $(n<=10)$ 而彼此不受攻击（即在棋盘的任一行，任一列和任一对角线上不能放置2个皇后），编程求解所有的摆放方法。

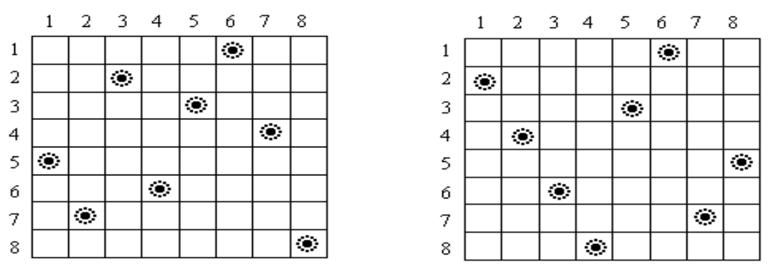
Input： $n$

Output：每行输出一种方案，每种方案顺序输出皇后所在的列号，每个数占5列。若无方案，则输出no solute!

Sample：

Input：       Output:
4                 2    4    1    3
                  3    1    4    2

思路：

我们需要建立 a[i]数组，表示第i行的皇后放在第a[i]列，以及bool类型的 b[]、c[]、d[]数组分别标记当前列，当前两条对角线是否可用，若为false即为存在冲突，不能在棋盘上摆皇后，进行剪纸，后续行不用进行这一列的搜索。因为是一行一行摆皇后的，所以皇后在行之间的冲突不需要标记。

其中，关于对角线的冲突标记，可以发现同一左对角线的格子下标 i+j为定值，同一右对角线的格子下标 i-j为定值。

代码

#include <iostream>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
 
int n;
int mp[10][10] = {0}; // 初始化棋盘
int a[20]; // 第i行的皇后放在第ai列
bool b[20], c[40], d[40]; // 标记当前列，当前左对角线，当前右对角线是否可用
bool foundSolution = false; // 标记有没有找到答案
 
void ans() {
    foundSolution = true;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (j == a[i]) printf("%5d",j);
            else;
        }
    }
    cout << endl; // 输出整个棋盘后再换行一次
}
 
void dfs(int i) {
    for (int j = 1; j <= n; j++) {
        if (b[j] && c[i + j] && d[i - j + n]) {   //必须全为真，才能在棋盘上摆皇后
            a[i] = j; // 第i行的皇后放在第j列
            b[j] = false;   //冲突标记
            c[i + j] = false;
            d[i - j + n] = false;
            if (i < n) dfs(i + 1);
            else ans();
            b[j] = true;
            c[i + j] = true;
            d[i - j + n] = true; // 回溯，回溯到这一列皇后摆放之前的情况，进行下一次放皇后
        }
    }
}
 
int main() {
    cin >> n; // 获取n个皇后
    memset(b, true, sizeof(b));
    memset(c, true, sizeof(c));
    memset(d, true, sizeof(d));
    dfs(1); // 开始摆放第一个皇后（第一行）
 
    if (!foundSolution) {
        cout << "no solute!" << endl;
    }
 
    return 0;
}

第二题全排列问题

输出自然数1到n所有不重复的排列，即n的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

Input ：n(1≤n≤9)

Output：由1～n组成的所有不重复的数字序列，每行一个序列。每个数字占5列。

Input                    Output
4                            1    2    3    4
                             1    2    4    3
                             1    3    2    4
                             1    3    4    2
                             1    4    2    3
                             1    4    3    2
                             2    1    3    4
                             2    1    4    3
                             2    3    1    4
                             2    3    4    1
                             2    4    1    3
                             2    4    3    1 
                             3    1    2    4
                             3    1    4    2
                             3    2    1    4
                             3    2    4    1
                             3    4    1    2
                             3    4    2    1
                             4    1    2    3
                             4    1    3    2
                             4    2    1    3
                             4    2    3    1
                             4    3    1    2
                             4    3    2    1

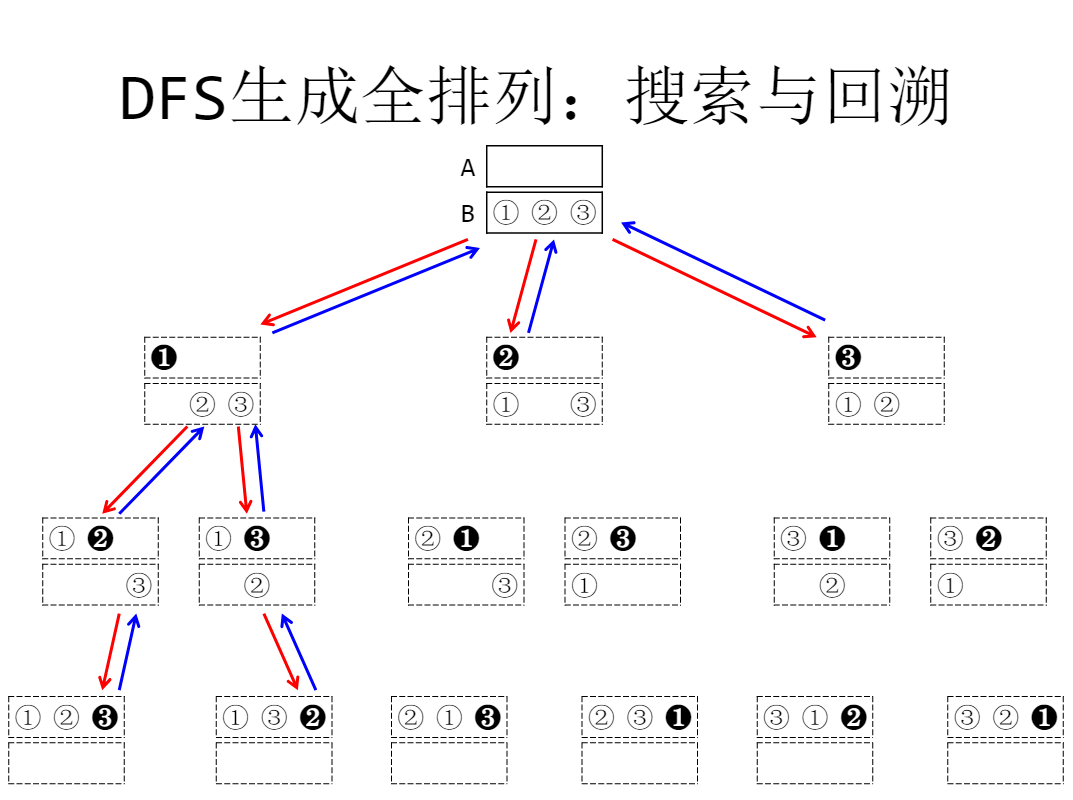
代码：

#include <stdio.h>

int a[10], b[10];

// 定义递归函数f，用于生成全排列
// n: 全排列的长度
// p: 当前排列的位置
void f(int n, int p) {
    // 如果当前排列位置p大于n，则表示已经生成了一个全排列
    if (p > n) {
        // 输出当前生成的全排列
        for (int i = 1; i <= n; i++) {
            printf("%5d", a[i]);
        }
        printf("\n");
        return;
    }

    // 循环遍历每个数字，尝试将其放到当前排列的位置p上
    for (int i = 1; i <= n; i++) {
        // 如果数字i还没有被使用（标记数组b中为1），则将其放到当前排列的位置p上
        if (b[i] == 0) continue;
        b[i] = 0; // 标记数字i已经被使用
        a[p] = i; // 将数字i放到当前排列的位置p上
        f(n, p + 1); // 递归调用f，生成下一个位置的排列
        b[i] = i; // 恢复数字i的可用状态
        a[p] = 0; // 清空当前排列的位置p上的数字
    }
}

int main() {
    int n;
    scanf("%d", &n);

    // 初始化标记数组b，表示数字1到n都可用
    for (int i = 1; i <= n; i++) {
        b[i] = i;
    }

    // 调用递归函数f，生成全排列
    f(n, 1);

    return 0;
}

第四天8月3日：广度优先搜索(Breadth-First-Search,BFS)

第一题 A - 马的遍历

有一个 $n \times m$ 的棋盘，在某个点 $(x, y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

Input：输入只有一行四个整数，分别为 $n, m, x, y$ 。

Output：一个 $n \times m$ 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 $-1$ ）。

Sample

Input             Output
3 3 1 1           0    3    2  
                  3    -1   1  
                  2    1    4

对于全部的测试点，保证 $1 \leq x \leq n \leq 400$ ， $1 \leq y \leq m \leq 400$ 。

代码

#include <bits/stdc++.h>
using namespace std;
int n, m; // n行, m列
int dir[][2] = {{-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}}; // 搜索的方向向量
int mp[405][405]; // 存储每个位置到起点的最短距离

//位置的结构体
struct pos {
    int r, c, d; // r行，c列，d表示距离
    pos(int a = 0, int b = 0, int d = 0) : r(a), c(b), d(d) {}
};

queue<pos> q; // 定义队列，用于广度优先搜索
void bfs(int r, int c); // 定义广度优先搜索函数

int main() {
    int sr, sc;
    cin >> n >> m >> sr >> sc; // 输入地图的行数n，列数m，以及起点坐标sr和sc
    memset(mp, -1, sizeof mp); // 初始化mp数组为-1
    bfs(sr, sc); // 进行广度优先搜索，计算每个位置到起点的最短距离

    // 输出每个位置到起点的最短距离
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cout << mp[i][j] << '\t';
        }
        cout << endl;
    }
    return 0;
}

void bfs(int r, int c) {
    q.push(pos(r, c, 0)); // 起点入队，并将其距离设为0
    mp[r][c] = 0; // 将起点的最短距离设为0

    while (!q.empty()) {
        pos p = q.front(); // 取队首，并出队
        q.pop();

        for (int i = 0; i < 8; i++) {
            int nr = p.r + dir[i][0]; // 新行
            int nc = p.c + dir[i][1]; // 新列
            int nd = p.d + 1; // 新的距离为原距离加1

            if (nr >= 1 && nr <= n && nc >= 1 && nc <= m && mp[nr][nc] == -1) {
                mp[nr][nc] = nd; // 更新新位置的最短距离
                q.push(pos(nr, nc, nd)); // 将新位置入队
            }
        }
    }
}

从给定起点出发，使用广度优先搜索算法计算每个位置到起点的最短距离，并将结果输出。其中，mp数组用于存储每个位置到起点的最短距离，初始值为-1表示尚未计算。bfs函数用于进行广度优先搜索，通过遍历8个方向的相邻位置，将最短距离不断更新，并将新位置加入队列，直到队列为空为止。最后输出每个位置到起点的最短距离。

第二题 Lake Counting S

由于近期的降雨，雨水汇集在农民约翰的田地不同的地方。我们用一个 $N\times M(1\leq N\leq 100, 1\leq M\leq 100)$ 的网格图表示。每个网格中有水（W）或是旱地（.）。一个网格与其周围的八个网格相连，而一组相连的网格视为一个水坑。约翰想弄清楚他的田地已经形成了多少水坑。给出约翰田地的示意图，确定当中有多少水坑。

输入第 $1$ 行：两个空格隔开的整数： $N$ 和 $M$ 。

第 $2$ 行到第 $N+1$ 行：每行 $M$ 个字符，每个字符是 W 或 .，它们表示网格图中的一排。字符之间没有空格。

输出一行，表示水坑的数量。

Due to recent rains, water has pooled in various places in Farmer John's field, which is represented by a rectangle of N x M (1 <= N <= 100; 1 <= M <= 100) squares. Each square contains either water ('W') or dry land ('.'). Farmer John would like to figure out how many ponds have formed in his field. A pond is a connected set of squares with water in them, where a square is considered adjacent to all eight of its neighbors. Given a diagram of Farmer John's field, determine how many ponds he has.

Input：

Line 1: Two space-separated integers: N and M * Lines 2..N+1: M characters per line representing one row of Farmer John's field. Each character is either 'W' or '.'. The characters do not have spaces between them.

Output：

Line 1: The number of ponds in Farmer John's field.

Sample：

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

提示

OUTPUT DETAILS: There are three ponds: one in the upper left, one in the lower left, and one along the right side.

代码

#include <iostream>
#include <queue>
using namespace std;
int n,m; // n行，m列
char mp[105][105];
//八个方向，左、左上、上、右上、右、右下、下、左下
int dir[][2]={{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1},{0,-1},{-1,-1}};
struct pos{
    int r,c; //r行，c列
};
void bfs(pos p);
int main() {
    cin >> n >> m;
    //获取地图信息
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin >> mp[i][j];
        }
    }
    int cnt = 0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(mp[i][j] == 'W') {
                bfs((pos){i,j});
                cnt ++;
            }
        }
    }
    cout << cnt << endl;
    return 0;
}
void bfs(pos p){
    queue<pos> q;
    //起点入队，并标记为干地
    q.push(p);
    mp[p.r][p.c] = '.';
    while(!q.empty()){
        //取队首，并出队
        pos p1 = q.front();
        q.pop();
        for(int i = 0;i < 8;i++){
            int nr = p1.r + dir[i][0];     //新行
            int nc = p1.c + dir[i][1];     //新列
            if(nr >= 1 && nr <= n && nc >=1 && nc <= m && mp[nr][nc]=='W'){
                q.push((pos){nr,nc});
                mp[nr][nc] = '.';
            }
        }
    }
}

昵称

邮箱

网址

按正序
按倒序
按热度

暑假集训第四篇周记（7月31日-8月6日）

每日知识点

第一天 7月31日：贪心算法 (Greedy)

第二天 8月1日：二叉树、深搜（DFS）、宽搜（BFS）、堆

二叉树：

二叉树的遍历

第三天8月2日：深度优先搜索（Depth-First-Search,DFS）

第四天8月3日：广度优先搜索(Breadth-First-Search,BFS)

部分题目详细分析与总结

第一天7月31日：贪心算法

第一题部分背包问题

第二天8月1日：二叉树、深搜、宽搜、堆

第一题：[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

第二题：堆（模板）

第三天8月2日：深度优先搜索（Depth-First-Search,DFS）

第一题 N皇后问题（模板题、经典）

第二题全排列问题

第四天8月3日：广度优先搜索(Breadth-First-Search,BFS)

第一题 A - 马的遍历

第二题 Lake Counting S

预览: