暑假集训第三篇周记(7月24日-7月30日)
摘要
涉及内容:尺取法、二分法、前缀和差分、倍增法与ST算法
每日知识点
第一天7月24日: 尺取法
尺取法(又称双指针、Two Pointers)
- 应用背景:
- 给定一个序列,有时需要它是有序的,先排序;
- 问题和序列的区间相关,且需要操作两个变量,可以用两个下标(指针)和扫描区间。
- 降低双重循环时间复杂度由变为
- 相较于哈希法,哈希法更快,但是需要一个额外很大的哈希空间
尺取法分为两种,即和存在两种扫描方向:
- 反向扫描:和方向相反,从头到尾,从尾到头,在中间相会。(左右指针)
- 同向扫描 (滑动窗口):和方向相同,都是从头到尾,但是速度不同,如:的速度更快一些(快慢指针)
第二天7月25日:二分法
应用背景:
根的存在性:函数在闭区间上连续,单调递增
算法竞赛中有两种题型:整数二分、实数二分
整数二分
基本代码:
在给出单调递增序列中找或的后继
int bin_search(int *a,int n,int x){ //a[0]~a[n-1]是单调递增的
int left = 0,right = n; //注意:不是n-1,此时是左闭右开的[0,n)
while(left < right){
int mid = left + (right - left)/2; //int mid = (left + right) >> 1;
if(a[mid]>=x) right = mid;
else left = mid + 1; //终止于left = right
}
return left;
}
| 实现 | 适用场合 | 可能出现的问题 |
|---|---|---|
| mid=(left+right)/2 | left≥0,right≥0,left+right无溢出 | 1. left+right 可能溢出 2. 负数情况下有向0取整问题 |
| mid = left + (right - left)/2 | left - right 无溢出 | 若right和left都是大数且一正一负,right - left可能溢出 |
| mid = (left + right) >>1 | left + right 无溢出 | 若left 和 right都是大数,left + right 可能溢出 |
代码中的 left = mid + 1不能写成 left = right
整数二分存在取整问题,如原值left = 2, right = 3,计算得mid = left + (right - left)/2 = 2,若取left = right,那么新的值仍然是left = 2,right = 3,while()陷入了死循环。如果写成left = mid + 1, 就不会死循环。
在给出单调序列中找或的前驱
int bin_search(int *a,int n, int x){ //a[0]~a[n-1]是单调递增的
int left = 0,right = n;
while(left < right){
int mid = left + (right + left + 1) / 2; //int mid = left + (right + left + 1) >> 1;
if(a[mid] <= x) left = mid;
else right = mid -1;
}
return left; ////终止于left = right
}
整数二分的建模:基本形式如下:
while(left < right){
int ans; //记录答案
int mid = left + (right - left)/2; //二分
if(check(mid)){ //检查条件,如果成立
ans = mid; //记录答案
... //移动left(right)
}
else ... //移动left(right)
}
二分法的难点在于如何建模和 check()函数检查条件,其中可能会套用其他算法或者数据结构
实数二分
因为没有涉及到取整的问题,编码比整数二分简单。其基本形式如下:
const double eps = 1e-7; //精度,如果下面用for可以不要eps
while((right - left) > eps){ //for(int i=0;i<100;i++){
double mid = left + (right - left) / 2;
if(check(mid)) right = mid; //判定,然后继续二分
else left = mid;
}
第三天7月26日:前缀和差分
前缀和
概念:数组a[0]~a[n-1],前缀和 sum[i] = a[0]~a[i] 的和
利用递推,可以在时间内求得所有前缀和:sum[i] = sum[i-1] + a[i]
如果预计算出前缀和,就能利用它快速计算出数组中任意区间 到 的和,即:
a[i] + a[i+1] +...+a[j+1]+a[j] = sum[j] - sum[i-1]
差分
差分是前缀和的逆运算,差分是一种处理数据的巧妙而简单的方法,它应用于区间的修改和询问问题。引入差分数组D,当修改某个区间时,只需要修改这个区间的端点,就可以记录整个区间的修改。差分分为一维差分、二维差分、三位差分
一维差分
讨论以下场景:
- 给定一个长度为n的一维数组a[ ],数组内的每个元素有初始值
- 修改操作:做m次区间修改,每次修改对区间内所有元素做相同的加减操作
- 询问操作:询问每一个元素的新值是多少
在差分法中,用到了两个数组:原数组a[ ] 和差分数组D[ ]
差分数组D[ ]的定义是 D[k] = a[k] - a[k-1],即原数组a[ ]的相邻元素的差。从定义中可以推出:
也就是说,a[ ]是D[ ]的前缀和。这个公式揭示了a[ ]和D[ ]的关系——“差分是前缀和的逆运算”,它把求a[k]转换为求D的前缀和。
把数组区间内的每个元素a[ ]加上d,只需要对相应的D[ ]做以下操作:
- 把加上:+=;
- 把减去:-=。
利用D[ ]能精准地实现只修改区间内元素的目的,而不会改变区间外a[ ]的值。因为前缀和 a[k] = D[1]+D[2]+...+D[k]有:
- ,前缀和不变;
- ,前缀和增加了;
- ,前缀和不变,因为被中减去的抵消了
二维差分
定义:在二维情况下,差分变成了相邻的的“面积差”,计算公式为:
区间修改:在一维情况下做区间修改时,只需要修改区间的值。在二维情况下,一个区间时一个小矩阵,有4个端点,需要修改这四个端点的值
D[x1][y1] +=d; //二维区间的起点
D[x1][y2+1] -=d; //把x看作常数,y从y1到y2+1
D[x2+1][y1] -=d; //把y看作常数,x从x1到x2+1
D[x2+1][y2+1] +=d; //由于前面把d减了两次,多减了一次,这里加一次回来
第四天 7月27日:倍增法与ST算法
倍增法(Binary Lifting)
主要应用场景:
- 从小区间扩大到大区间
- 从小数值扩大到大数值
原理:利用二进制本身的倍增性,把一个数用二进制展开,二进制划分反映了一种快速增长的特性,第位的权值等于前面所有权值的和+1。一个整数,它的二进制只有位。如果要从0增长到n,可以1,2,4,...,为“跳板”,快速跳到,这些跳板只有个。
倍增的经典题目:国旗计划 (洛谷P4155)
A 国正在开展一项伟大的计划 —— 国旗计划。这项计划的内容是边防战士手举国旗环绕边境线奔袭一圈。这项计划需要多名边防战士以接力的形式共同完成,为此,国土安全局已经挑选了 名优秀的边防战上作为这项计划的候选人。
A 国幅员辽阔,边境线上设有 个边防站,顺时针编号 至 。每名边防战士常驻两个边防站,并且善于在这两个边防站之间长途奔袭,我们称这两个边防站之间的路程是这个边防战士的奔袭区间。名边防战士都是精心挑选的,身体素质极佳,所以每名边防战士的奔袭区间都不会被其他边防战士的奔袭区间所包含。
现在,国十安全局局长希望知道,至少需要多少名边防战士,才能使得他们的奔袭区间覆盖全部的边境线,从而顺利地完成国旗计划。不仅如此,安全局局长还希望知道更详细的信息:对于每一名边防战士,在他必须参加国旗计划的前提下,至少需要多少名边防战士才能覆盖全部边境线,从而顺利地完成国旗计划。
输入格式:
第一行,包含两个正整数 ,,分别表示边防战士数量和边防站数量。
随后 行,每行包含两个正整数。其中第 行包含的两个正整数 、 分别表示 号边防战士常驻的两个边防站编号, 号边防站沿顺时针方向至 边防站力他的奔袭区间。数据保证整个边境线都是可被覆盖的。
输出格式:
输出数据仅 行,需要包含 个正整数。其中,第 个正整数表示 号边防战士必须参加的前提下至少需要多少名边防战士才能顺利地完成国旗计划。
思路:
首先考虑从一个区间出发,如何选择所有的区间。选择一个区间后,下一个区间只能从左端点小于或者等于的右端点的那些区间中选择,这些区间中选择右端点最大的那个区间是最优的。
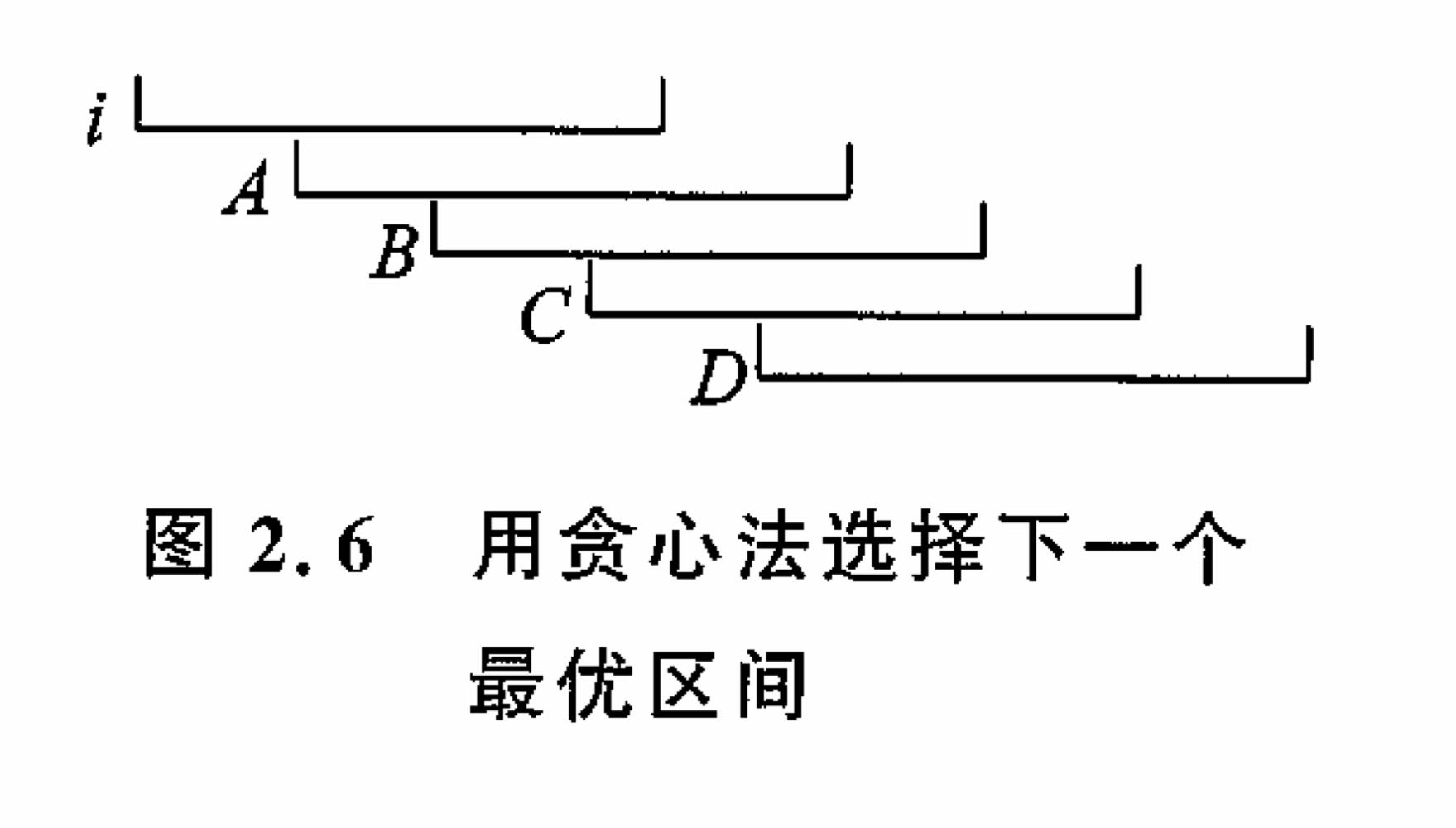
如图,选择区间后,下一个区间可以从区间A、B、C中选择,它们的左端点都在内部。C是最优的,因为它的右端点最远。为了快速的高效查询,使用倍增法,预计算出一些“跳板”,快速找到后面的区间。
定义 go[s][i]表示从第个区间出发,走个最优区间后到达的区间
注意
先跳大数后跳小数
计算 go[][]有以下递推关系
go[s][i] = go[go[s][i-1]][i-1] //先起跳2^i-1步,再跳2^i-1步,最终跳了2^i步
对于倍增法,它的核心思想是将原本复杂的问题划分为一系列简单的子问题,并利用已经计算出来的中间结果来加速计算。在 go 数组中,go[s][i] 表示从位置 s 起跳 2^i 步后的位置。
现在,来详细解释一下为什么会有已经计算出来的中间结果存在,以及它们是如何使用的。
初始化:在倍增法的预处理阶段,首先计算出
go[s][0]的值。这是因为从位置s起跳2^0步后,其位置还是s本身。所以go[s][0] = s。递推计算:接下来,利用动态规划的思想,通过递推计算出
go[s][i],其中i > 0。a.
go[s][i]表示从位置s起跳2^i步后的位置。为了得到这个结果,需要利用已经计算出来的中间结果,即go[s][i-1]和go[go[s][i-1]][i-1]。b.
go[s][i-1]表示从位置s起跳2^(i-1)步后的位置。这个值已经在之前的计算中得到了。c.
go[go[s][i-1]][i-1]表示从位置go[s][i-1]起跳2^(i-1)步后的位置。由于已经知道go[s][i-1]的值,所以可以直接查表得到go[go[s][i-1]][i-1]的值。d. 综上所述,通过查表可以在
O(1)时间内得到go[s][i]的值,因为它只涉及已经计算出来的中间结果go[s][i-1]和go[go[s][i-1]][i-1]。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5+1;
int n,m;
struct warrior{
int id,L,R; //id为战士的编号;L和R为战士的左右区间
bool operator<(const warrior b) const{return L < b.L;}
}w[N*2];
int n2;
int go[N][20];
void init(){ //贪心 + 预计算倍增
int nxt = 1;
for(int i = 1;i<=n2;i++){ //用贪心求每个区间的下一个区间
while(nxt <= n2 && w[nxt].L<=w[i].R)
nxt++; //每个区间的下一个区间是右端点最大的区间
go[i][0] = nxt - 1; //区间i的下一个区间
}
for(int i=1;(1<<i)<=n;++i) //倍增:i=1,2,4……
for(int s=1;s<=n2;s++) //每个区间后的第2^i个区间
go[s][i] = go[go[s][i-1]][i-1];
}
int res[N];
void getans(int x){ //从第x个战士出发
int len = w[x].L+m,cur = x,ans=1;
for(int i= log2(N);i>=0;i--){ //从最大的i开始找:2^i = N
int pos = go[cur][i];
if(pos && w[pos].R<len){
ans += 1 << i; //累加跳过的区间
cur = pos; //从新的位置继续开始
}
}
res[w[x].id] = ans + 1;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
w[i].id = i; //记录战士的顺序
scanf("%d%d",&w[i].L,&w[i].R);
if(w[i].R<w[i].L) w[i].R += m;
}
sort(w+1,w+1+n);
n2 = n;
for(int i=1;i<=n;i++){
n2++;
w[n2] = w[i];
w[n2].L = w[i].L + m;
w[n2].R = w[i].R + m;
}
init();
for(int i=1;i<=n;i++) getans(i);
for(int i=1;i<=n;i++) printf("%d ",res[i]);
return 0;
}
其中,有一个循环 for (int i = 1; (1 << i) <= n; ++i),它的作用是找到最大的 i,使得 2^i <= n 成立。现在逐步解释这个循环:
1 << i:这是一个左移操作,表示将数字 1 左移i位。在二进制表示中,左移i位就相当于乘以2^i。例如,当i等于 1 时,1 << i就是二进制的 10,即十进制的 2。当i等于 2 时,1 << i就是二进制的 100,即十进制的 4,以此类推。(1 << i) <= n:这是一个条件判断,判断1 << i是否小于等于n。如果满足这个条件,循环继续执行,否则循环结束。也就是说,循环会一直进行,直到1 << i大于n。++i:这是i的自增操作,使得i的值每次循环都加 1。
这个循环的作用:
假设 n 是一个正整数,我们希望找到最大的 i,使得 2^i <= n。这其实就是找到最大的 i,使得 2^i 不超过 n,同时也就是找到最大的 i,使得 2^(i+1) 超过 n。
例如,当 n 等于 5 时,满足条件的最大 i 是 2,因为 2^2 等于 4(不超过 5),而 2^3 等于 8(超过 5)。
这个循环的目的是为了找到最大的 i,使得 2^i 不超过 n,这样在预处理中我们可以使用 1 << i 作为一个合理的步长,方便地进行一些二进制运算。在这个代码中,正是利用这个特性来计算 go 数组的第二维大小。由于 go 数组的大小是固定的,因此需要找到一个合适的值来作为第二维的大小。通过这个循环,找到了最大的 i,使得 2^i 不超过 n,然后将 i 的值作为 go 数组第二维的大小,即 go[N][20],其中 N 是 4e5+1。
ST算法(Sparse Table)
ST算法是基于倍增原理的算法。ST算法源于这样一个原理:一个大区间若能被两个小区间覆盖,那么大区间的最值等于两个小区间的最值。例:大区间{4,7,9,6,3,6,4,8,7,5}被两个小区间{4,7,9,6,3,6,4,8}和{4,8,7,5}所覆盖,大区间的最小值为3,等于两个小区间的最小值,即min{3,4}为3。
提示
这个例子特意让两个小区间有所重合,因为重合不影响结果。
从以上原理得到ST算法的基本思路,包括两个步骤:
- 把整个数列分为很多个小区间,并提前计算出每个小区间的最值;
- 对任意区间最值查询,找到覆盖它的两个小区间,由两个小区间的最值算出答案。
每组的小区间最值,可以从前一组递推而来,定义 dp[s][k]表示左端点为,区间长度为的区间最值。递推关系为:
dp[s][k] = min(dp[s][k - 1],dp[s + 1 << (k - 1)][k - 1]); //1<<(k-1)表示2^(k-1)
在任意区间中,有以任意元素为起点的小区间,也有以任意元素为终点的小区间。根据这个结论,可以把需要查询的区间[L,R]分为两个小区间,且这两个小区间属于同一区间:以L为起点的小区间、以R为终点的小区间。区间[L,R]的长度为 len = R - L +1两个小区间的长度都为x,令x为比len小的2的最大倍数,有x≤len且2x≥len,这样保证能覆盖。另外需要计算 dp[][],根据 dp[s][k]的定义,有。例如,, ,,。
已知,如何求?
int k = (int)(log(double(R-L+1))/log(2.0));
int k = log2(R-L+1);
最后给出区间[L,R]最小值的计算公式,等于覆盖它的两个小区间的最小值,即:
min(dp[L][k], dp[R-(1 << k)+1][k])
第五天7月28日:排序与排列
排序函数
常见的排序算法如表:
| 排序算法 | 时间复杂度 | 原理 |
|---|---|---|
| 选择排序 | 比较 | |
| 插入排序 | 比较 | |
| 冒泡排序 | 比较 | |
| 归并排序 | 比较、分治 | |
| 快速排序 | ,不稳定 | 比较、分治 |
| 堆排序 | 比较、分治 | |
| 计数排序 | ,不稳定 | 对数值按位划分 |
| 基数排序 | 对数值按位划分 | |
| 桶排序 | 对数值分类、分治 |
不过在算法竞赛中,一般不需要自己写这些排序算法,而是直接使用库函数。
排列
STL的 next_permutation()已在周记第二篇中写过,详见
部分题目详细分析与总结
第一天 7月24日:尺取法
第一题:A - Palindromes _easy version (反向扫描)
“回文串”是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串。请写一个程序判断读入的字符串是否是“回文”。
Input:输入包含多个测试实例,输入数据的第一行是一个正整数n,表示测试实例的个数,后面紧跟着是n个字符串。
Output:如果一个字符串是回文串,则输出"yes",否则输出"no".
Sample:
Input: Output:
4 yes
level no
abcde yes
noon no
haha
#include <iostream>
#include <string>
using namespace std;
int main()
{
int n;
cin >> n;
while(n--){
string s;
cin >> s;
bool ans = true;
int i = 0, j = s.size() - 1;
while(i<j){
if(s[i] != s[j]){
ans = false;
break;
}
i++;
j--;
}
if(ans) cout << "yes" << endl;
else cout << "no" << endl;
}
return 0;
}
第二题:C - Subsequence (同向扫描)
A sequence of N positive integers (10 < N < 100 000), each of them less than or equal 10000, and a positive integer S (S < 100 000 000) are given. Write a program to find the minimal length of the subsequence of consecutive elements of the sequence, the sum of which is greater than or equal to S.
Input:
The first line is the number of test cases. For each test case the program has to read the numbers N and S, separated by an interval, from the first line. The numbers of the sequence are given in the second line of the test case, separated by intervals. The input will finish with the end of file.
Output:
For each the case the program has to print the result on separate line of the output file.if no answer, print 0.
思路:是寻找区间和的变形题
- 初始值 = , = ,即都开始指向第一个元素。定义是区间数组元素的和,初始值 = 。
- 如果,把后移一位,并让加上这个值
- 如果, 让减掉元素,并把后移一位,计算此时最小的区间长度
Sample:
Input: Output:
2 2
10 15 3
5 1 3 5 10 7 4 9 2 8
5 11
1 2 3 4 5
#include <iostream>
#include <vector>
using namespace std;
int main() {
int T;
cin >> T;
while (T--) {
int N, S;
cin >> N >> S;
vector<int> s(N);
for (int i = 0; i < N; i++) {
cin >> s[i];
}
int minLength = N + 1;
int i = 0, j = 0;
int currentSum = 0;
while (j < N) {
if (currentSum < S) { //当前值小于目标s,移动快指针
currentSum += s[j];
j++;
} else {
minLength = min(minLength, j - i); //通过计算j - i来得到当前窗口的长度,然后与之前得到的minLength进行比较,保留较小的值
currentSum -= s[i]; //当前值大于目标值s,移动慢指针
i++;
}
}
while (currentSum >= S) { // 处理尾部剩余元素,如果窗口内的元素仍然满足条件,继续更新最小子序列长度
minLength = min(minLength, j - i);
currentSum -= s[i];
i++;
}
if (minLength == N + 1) { // 如果最小子序列长度仍然为N+1,说明整个序列和都不满足条件,输出0
cout << 0 << endl;
} else {
cout << minLength << endl;
}
}
return 0;
}
第二天7月25日:二分法
第一题:A - Pie (实数二分-最小值最大化问题)
My birthday is coming up and traditionally I'm serving pie. Not just one pie, no, I have a number N of them, of various tastes and of various sizes. F of my friends are coming to my party and each of them gets a piece of pie. This should be one piece of one pie, not several small pieces since that looks messy. This piece can be one whole pie though. My friends are very annoying and if one of them gets a bigger piece than the others, they start complaining. Therefore all of them should get equally sized (but not necessarily equally shaped) pieces, even if this leads to some pie getting spoiled (which is better than spoiling the party). Of course, I want a piece of pie for myself too, and that piece should also be of the same size. What is the largest possible piece size all of us can get? All the pies are cylindrical in shape and they all have the same height 1, but the radii of the pies can be different.
Input
- One line with two integers N and F with 1 ≤ N, F ≤ 10 000: the number of pies and the number of friends.
- One line with N integers ri with 1 ≤ ri ≤ 10 000: the radii of the pies.
Output
For each test case, output one line with the largest possible volume V such that me and my friends can all get a pie piece of size V. The answer should be given as a floating point number with an absolute error of at most 10−3.
Sample
Input Output
3 25.1327
3 3 3.1416
4 3 3 50.2655
1 24
5
10 5
1 4 2 3 4 5 6 5 4 2
代码
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdio>
#define eps 1e-5
#define PI 3.14159265358979323846
double area[10010];
using namespace std;
bool check(double mid, int N, int F);
int main() {
int T;
cin >> T; //T组数据
while (T--) {
int N, F;
cin >> N >> F; //获得我有N个Pie,F个朋友
for (int i = 0; i < N; i++) {
int r;
cin >> r;
area[i] = PI * r * r; //计算Pie的面积并存储在area数组中
}
sort(area, area + N); //对面积数组进行排序
double left = 0, right = area[N - 1];
while ((right - left) > eps) {
double mid = left + (right - left) / 2;
if (check(mid, N, F))
left = mid;
else
right = mid;
}
printf("%.4f\n", left);
}
return 0;
}
bool check(double mid, int N, int F) {
int sum = 0;
for (int i = 0; i < N; i++) {
sum += floor(area[i] / mid); //使用floor函数向下取整
}
if (sum >= F + 1)
return true;
else
return false;
}
第二题:D - 进击的奶牛 (整数二分)
Farmer John 建造了一个有≤≤个隔间的牛棚,这些隔间分布在一条直线上
他的≤≤)头牛不满于隔间的位置分布,它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的互相打斗,Farmer John 想把这些牛安置在指定的隔间,所有牛中相邻两头的最近距离越大越好。那么,这个最大的最近距离是多少呢?
Input
第 11 行:两个用空格隔开的数字 和 。
第 ∼ 行:每行一个整数,表示每个隔间的坐标。
Output
输出只有一行,即相邻两头牛最大的最近距离。
Sample
Input Output
5 3 3
1
2
8
4
9
代码
#include <iostream>
#include <algorithm>
using namespace std;
int N,C,x[100005]; //N个牛棚,C头牛,牛棚坐标
bool check(int dis){
int cnt=1, place = 0;
for(int i = 1;i<N;++i){
if(x[i] - x[place] >= dis){
cnt++;
place = i;
}
}
if(cnt >= C) return true;
else return false;
}
int main() {
cin >> N >> C;
for(int i=0;i<N;i++){
cin >> x[i];
}
sort(x,x+N); //对牛棚坐标排序找到最远的牛棚
int left = 0, right = x[N-1] - x[0];
int ans = 0;
while(left < right){
int mid = left + (right - left) / 2;
if(check(mid)){
ans = mid;
left = mid + 1;
}
else right = mid;
}
cout << ans;
return 0;
}
第三天7月26日:前缀和差分
第一题:A - Color the ball (一维差分)
N个气球排成一排,从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了,你能帮他算出每个气球被涂过几次颜色吗?
Input
每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行,每行包括2个整数a b(1 <= a <= b <= N)。 当N = 0,输入结束。
Output
每个测试实例输出一行,包括N个整数,第I个数代表第I个气球总共被涂色的次数。
Sample
| Input | Output |
|---|---|
| 3 1 1 2 2 3 3 3 1 1 1 2 1 3 0 | 1 1 1 3 2 1 |
代码
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 100010;
int a[N],D[N]; //a是气球,D是差分数组
int main() {
int n;
while(~scanf("%d",&n)){
memset(a,0,sizeof(a)); //将a数组和D数组中的所有元素初始化为0
memset(D,0,sizeof(D));
for(int i=1;i<=n;i++){
int L,R;
scanf("%d%d",&L,&R);
D[L]++;
D[R+1]--; //区间修改
}
for(int i=1;i<=n;i++){ //求原数组
a[i] = a[i-1] + D[i]; //差分,求前缀和a[],a[i]就是气球i的值
if(i!=n) printf("%d ",a[i]);
else printf("%d\n",a[i]);
}
}
return 0;
}
第二题:E - 海底高铁
该铁路经过 个城市,每个城市都有一个站。不过,由于各个城市之间不能协调好,于是乘车每经过两个相邻的城市之间(方向不限),必须单独购买这一小段的车票。第 段铁路连接了城市 和城市 (≤i<)。如果搭乘的比较远,需要购买多张车票。第 段铁路购买纸质单程票需要博艾元。
虽然一些事情没有协调好,各段铁路公司也为了方便乘客,推出了 IC 卡。对于第段铁路,需要花博艾元的工本费购买一张 IC 卡,然后乘坐这段铁路一次就只要扣元。IC 卡可以提前购买,有钱就可以从网上买得到,而不需要亲自去对应的城市购买。工本费不能退,也不能购买车票。每张卡都可以充值任意数额。对于第 段铁路的 IC 卡,无法乘坐别的铁路的车。
Uim 现在需要出差,要去 个城市,从城市 出发分别按照 ,,,⋯, 的顺序访问各个城市,可能会多次访问一个城市,且相邻访问的城市位置不一定相邻,而且不会是同一个城市。
现在他希望知道,出差结束后,至少会花掉多少的钱,包括购买纸质车票、买卡和充值的总费用。
Input
第一行两个整数,,。
接下来一行, 个数字,表示 。
接下来 行,表示第 段铁路的 ,,。
Output
一个整数,表示最少花费
Sample
Input Output
9 10 6394
3 1 4 1 5 9 2 6 5 3
200 100 50
300 299 100
500 200 500
345 234 123
100 50 100
600 100 1
450 400 80
2 1 10
代码
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<int> c(n + 1, 0); // 对标记数组初始化
int p1, p2;
if (m > 0) {
cin >> p1; //读取第一个城市
}
for (int i = 2; i <= m; i++) {
cin >> p2; //读取第二个城市
if (p1 < p2) { //如果第一个城市的编号比第二个城市的编号小,说明为从小到大经过,标记数组p1就+1
c[p1]++;
c[p2]--;
} else { //反之则为从大到小经过,标记数组p2+1,防止重复标记重复买票
c[p2]++;
c[p1]--;
}
p1 = p2; //用p1记录p2的城市编号,作为下一轮比较中的第一个城市
}
long long int sum = 0;
int a,b,C;
long long re = 0;
for(int i = 1;i <= n; i++){
sum += c[i];
cin >> a >> b >> C;
if(sum!=0) re += min(a*sum,b*sum+C);
}
if (m <= 1) {
re = 0;
}
cout << re << endl;
return 0;
}
本题有个大坑,因为经过的城市是乱序的,所以存在部分城市多次经过的情况,但无论经过多少次都只需要买一次票,这样才能保证花的钱最少。于是我们需要判断城市编号的大小,判断是否经过,新经过的城市就需要做标记。
所以从数字较大的城市到小的城市,数字大的减一,小的加1,这样经过小的城市的时候就知道接下来的那段铁路是被经过了多少次,而到了减一的城市之后接下来经过的铁路就不受刚才路牌的影响,因为原来加的被减了。
第四天7月27日:倍增法与ST算法
第一题:C - ST表 (模板题)
这是一道 ST 表经典题——静态区间最大值
请注意最大数据时限只有 0.8s,数据强度不低,请务必保证你的每次查询复杂度为 。若使用更高时间复杂度算法不保证能通过。
如果您认为您的代码时间复杂度正确但是 TLE,可以尝试使用快速读入:
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
函数返回值为读入的第一个整数。
快速读入作用仅为加快读入,并非强制使用。
Description
给定一个长度为 的数列,和 次询问,求出每一次询问的区间内数字的最大值。
Input
第一行包含两个整数,,分别表示数列的长度和询问的个数。
第二行包含 个整数(记为 ),依次表示数列的第 项。
接下来 行,每行包含两个整数 ,表示查询的区间为
Output
输出包含 行,每行一个整数,依次表示每一次询问的结果。
Sample
Input Output
8 8 9
9 3 1 7 5 6 0 8 9
1 6 7
1 5 7
2 7 9
2 6 8
1 8 7
4 8 9
3 7
1 8
代码
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
const int MAXN = 100005;
const int MAXK = 20; // log2(MAXN) + 1
int st[MAXN][MAXK];
inline int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int main() {
int N = read(), M = read();
vector<int> arr(N);
for (int i = 0; i < N; i++) {
arr[i] = read();
}
// 构建ST表
for (int i = 0; i < N; i++) {
st[i][0] = arr[i];
}
for (int k = 1; (1 << k) <= N; k++) {
for (int i = 0; i + (1 << k) <= N; i++) {
st[i][k] = max(st[i][k - 1], st[i + (1 << (k - 1))][k - 1]);
}
}
// 处理查询
while (M--) {
int l = read(), r = read();
l--; // 转换为0-based index
r--; // 转换为0-based index
int k = log2(r - l + 1);
int ans = max(st[l][k], st[r - (1 << k) + 1][k]);
printf("%d\n",ans);
}
return 0;
}
第五天7月28日:排序与排列
第一题:A - Who's in the Middle (快速排序)
FJ is surveying his herd to find the most average cow. He wants to know how much milk this 'median' cow gives: half of the cows give as much or more than the median; half give as much or less. Given an odd number of cows N (1 <= N < 10,000) and their milk output (1..1,000,000), find the median amount of milk given such that at least half the cows give the same amount of milk or more and at least half give the same or less.
Input
- Line 1: A single integer N
- Lines 2..N+1: Each line contains a single integer that is the milk output of one cow.
Output
- Line 1: A single integer that is the median milk output.
Sample
| Input | Output |
|---|---|
5 2 4 1 3 5 | 3 |
代码
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 10010;
int a[N];
int quicksort(int left,int right,int k){
int mid = a[left + (right - left )/2];
int i = left, j = right - 1;
while(i<=j){
while(a[i]<mid) ++i;
while(a[j]>mid) --j;
if(i<=j){
swap(a[i],a[j]);
++i;
--j;
}
}
if(left <= j && k <= j) return quicksort(left,j+1,k);
if(i<right && k>= i) return quicksort(i,right,k);
return a[k];
}
int main() {
int n;
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
int k = n/2;
printf("%d\n",quicksort(0,n,k));
return 0;
}